Series temporales complejas III, diagramas de fases
En este nuevo artículo de la serie sobre caracterización gráfica de series temporales procedentes de un sistema dinámico con dinámica caótica, voy a hablar de una forma de representar dichos sistemas en el dominio del espacio, de forma independiente del tiempo, el diagrama de fases. Con este tipo de diagramas, se pueden observar los atractores del sistema. Un atractor es un punto, una curva, en general, un conjunto de puntos al que convergen las ecuaciones del sistema, que nos permite hacernos una idea del comportamiento típico del mismo.
Si quieres empezar la serie por el principio, este es el enlace al comienzo de la serie de artículos sobre caracterización gráfica de series temporales complejas. En este otro enlace os podéis descargar el ejecutable y el código fuente del proyecto GraphStudy, escrito en CSharp con Visual Studio 2013.
Hasta ahora he utilizado como ejemplo la ecuación logística, de una sola dimensión. Los atractores unidimensionales no son muy interesantes, pues se encuentran limitados a una recta, así que en este artículo voy a utilizar series con más de una variable, generadas por sistemas de dos o tres ecuaciones diferenciales.
Comencemos por un atractor simple, con el sistema de ecuaciones siguiente:
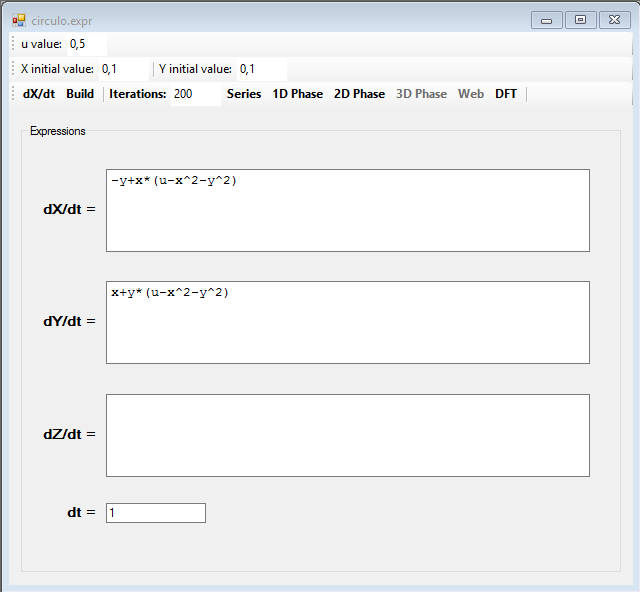
Las dos series están ligadas entre sí por las variables x e y, en esta imagen se pueden ver ambas series superpuestas, en rojo la serie para la variable x y en negro la de la variable y:
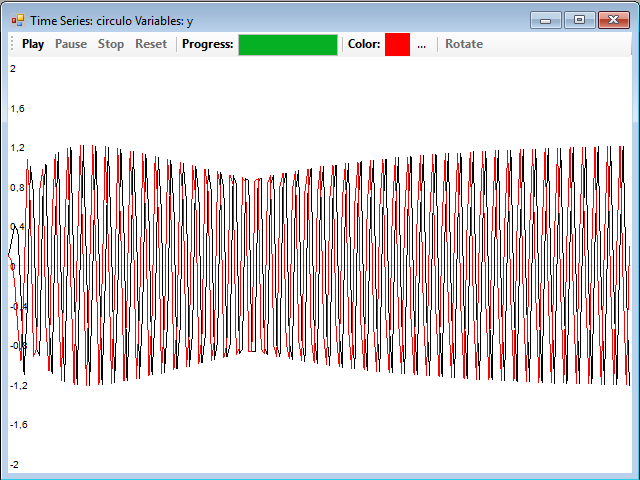
Para ver el atractor del sistema, solo hay que pulsar el botón 2D Phase y, en la ventana que aparece, el botón Play, para que se dibuje. Es conveniente utilizar un valor pequeño para dt, por ejemplo 0,001, y un número grande de iteraciones, por ejemplo 10000:
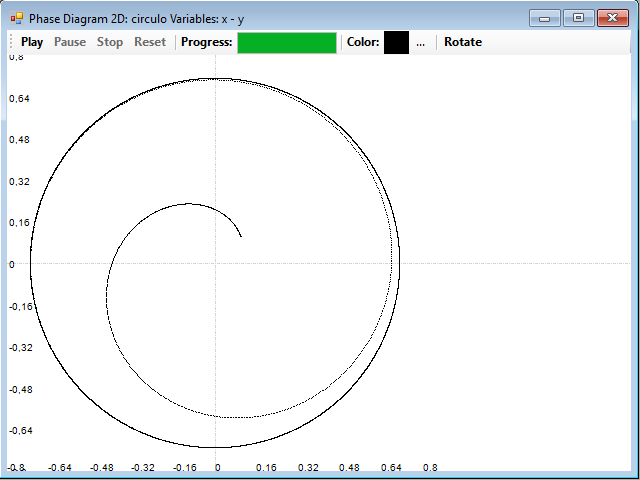
Trazar el diagrama de fases es sencillo, en cada paso calculamos el término correspondiente a cada una de las series, y dibujamos un punto en la gráfica que corresponda con esas coordenadas. Este sistema empieza en un punto cercano al origen (0,1, 0,1), y poco a poco va siguiendo una trayectoria hasta quedar confinado en un círculo. Este círculo es el atractor del sistema, la trayectoria del sistema hasta el círculo es el estado transitorio del sistema, y el círculo constituye lo que se llama su ciclo límite. Este es claramente un sistema periódico.
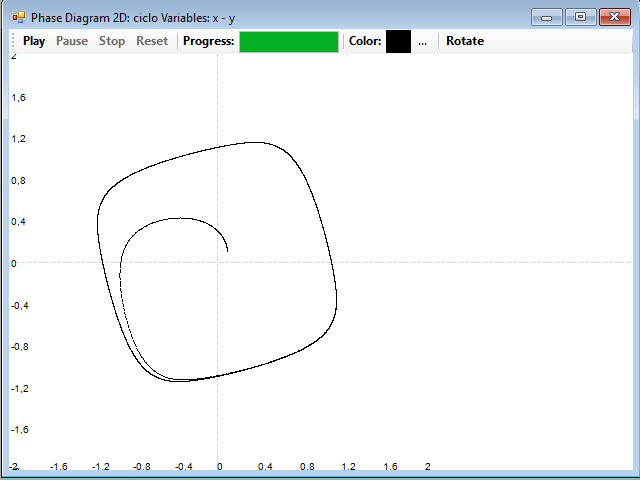
Otro ejemplo de ciclo límite lo podemos ver con este otro sistema de ecuaciones:
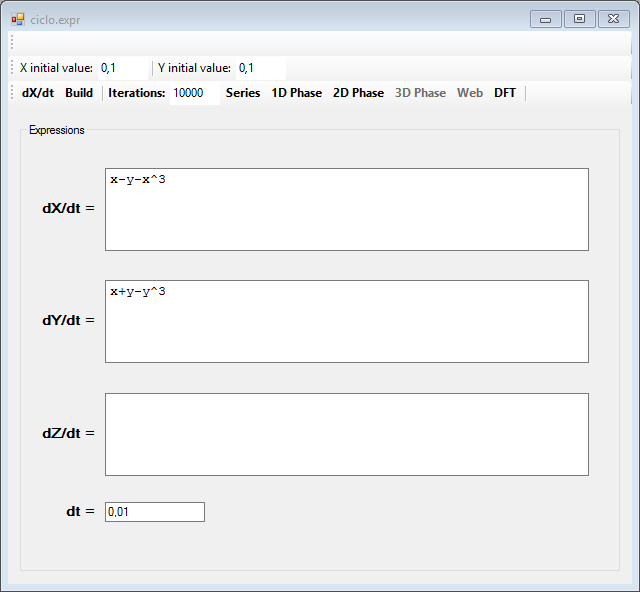
Y este es el ciclo límite que constituye su atractor:
Atractores extraños
En los sistemas de ecuaciones que presentan una dinámica compleja la cosa no es tan sencilla. Estos sistemas se caracterizan por tener atractores muy complejos, con infinidad de trayectorias, que forman un conjunto fractal de puntos, esto es, un conjunto cuya dimensión es un número fraccionario en lugar de un entero. A estos atractores se los denomina atractores extraños.
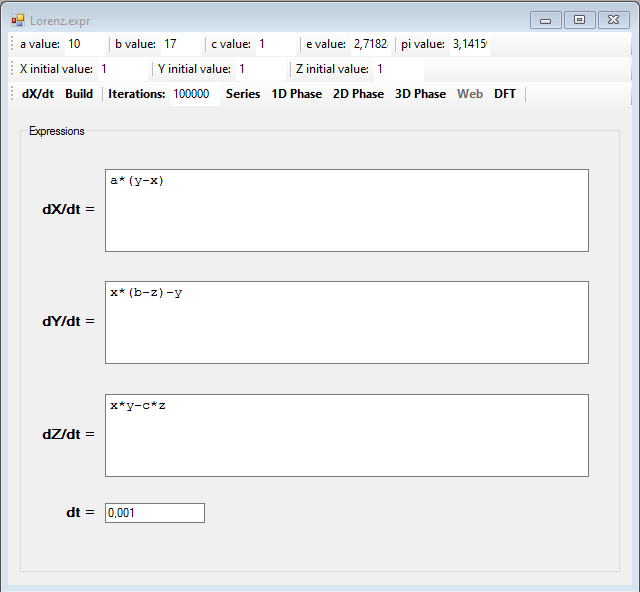
Un ejemplo clásico de sistema que presenta un atractor extraño es el modelo de Lorentz, que es un sistema de tres dimensiones, con tres ecuaciones diferenciales:
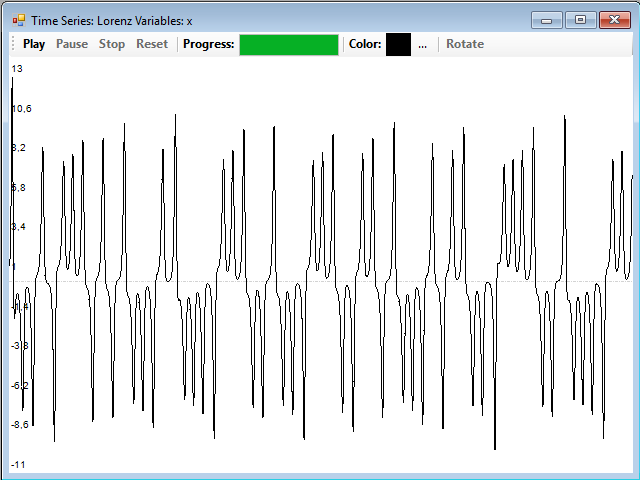
Las series correspondientes a las coordenadas x e y son muy similares, esta es la de la x:
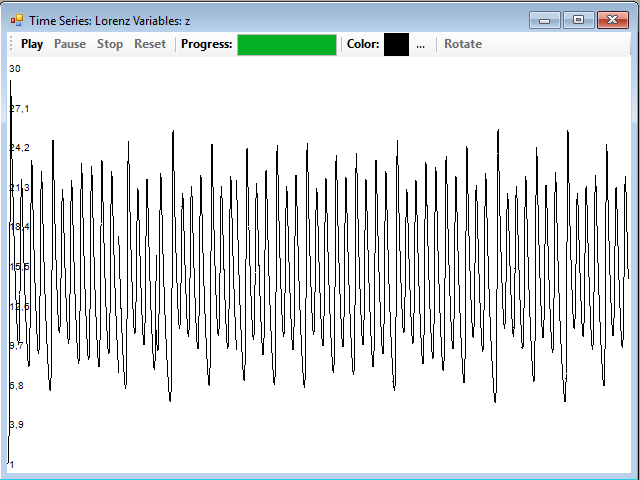
Y esta es la que corresponde a la coordenada z:
Para trazar el atractor de este sistema, pulsa el botón 3D Phase. Se obtiene el conocido atractor de Lorenz, con forma de mariposa:
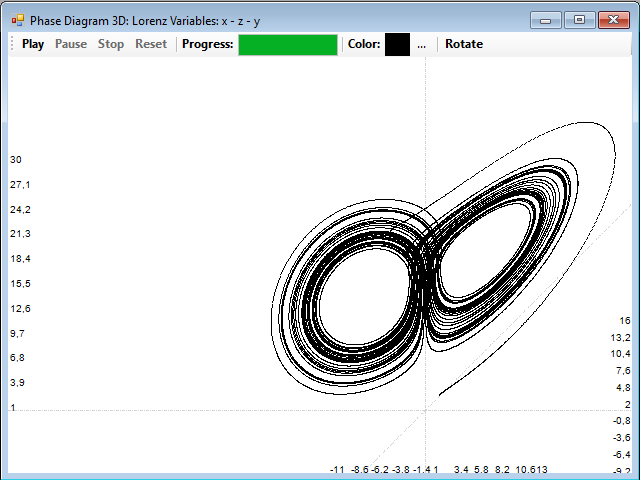
Con el botón Rotate se pueden variar las posiciones de los ejes de coordenadas para poder ver el atractor desde diferentes perspectivas. Este atractor presenta características típicas de los sistemas complejos. Tiene una dimensión algo mayor que 2, se estima que entre 2,05 y 2,07, con una estructura fractal, presenta invariancia de escala, pues por mucho que ampliemos una zona en la que se encuentren un grupo de trayectorias, encontraremos siempre un trazado similar también con múltiples trayectorias.
Otro sistema con un atractor extraño es el llamado sistema de Rössler, compuesto por las siguientes ecuaciones diferenciales:
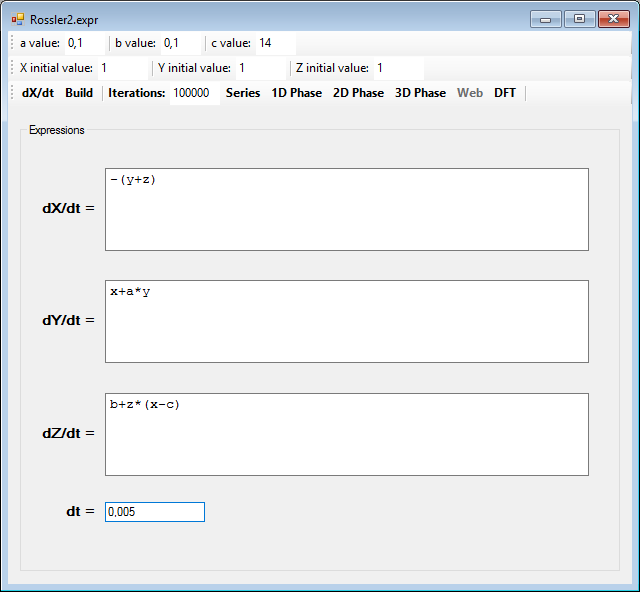
Y este es el atractor en tres dimensiones del sistema, el atractor de Rössler:
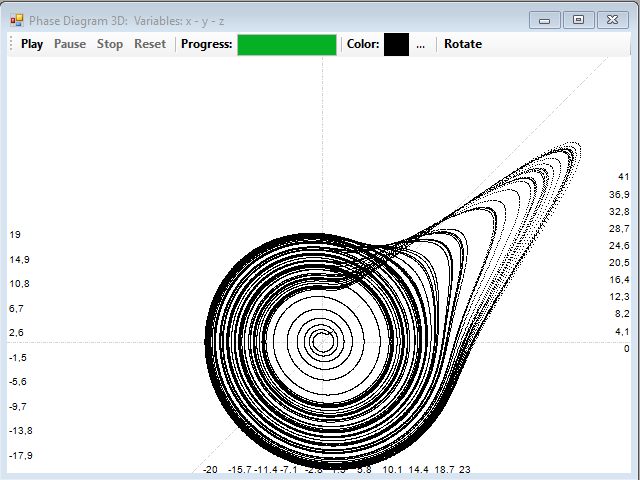
Decimos que estos sistemas presentan caos determinista, pues, aunque su dinámica es caótica, están generados por sistemas de ecuaciones totalmente deterministas.
Como puedes ver, resulta fácil distinguir una dinámica periódica de una dinámica caótica dibujando el diagrama de fases correspondiente a las series. Si estas son aleatorias y no están correlacionadas, lo que obtendremos será una nube de puntos sin forma definida, como la siguiente:
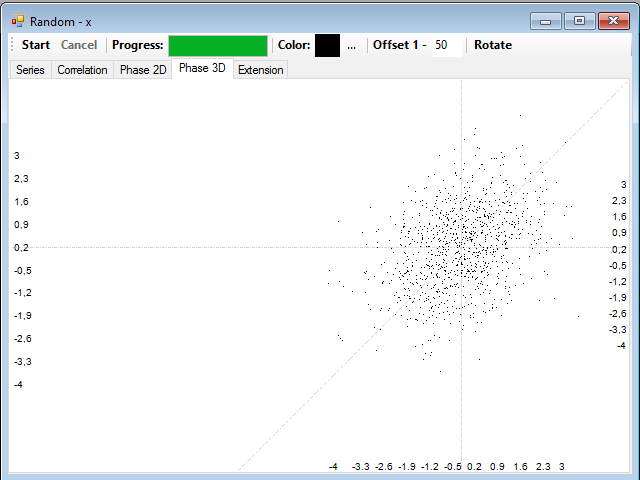
En el próximo artículo de la serie hablaré del espectro de potencia y distribución de valores.









