Series temporales complejas II, diagramas de recurrencia
Continuamos con la serie sobre caracterización gráfica de la complejidad en series temporales utilizando la aplicación auxiliar GraphStudy. En este artículo voy a mostrar cómo construir un gráfico con el que podemos distinguir de manera sencilla si una determinada función iterada genera series con una dinámica caótica, el diagrama de recurrencia.
Si quieres empezar la serie por el principio, este es el enlace al comienzo de la serie de artículos sobre caracterización gráfica de series temporales complejas. En este otro enlace os podéis descargar el ejecutable y el código fuente del proyecto GraphStudy, escrito en CSharp con Visual Studio 2013.
Continuando con la ecuación logística, que, recordemos, genera la siguiente serie:
Xn+1 = µXn(1-Xn)
Que presenta dinámica periódica cuando µ vale entre 3 y aproximadamente 3,5 y dinámica caótica a partir de este último valor, podemos generar el siguiente diagrama:
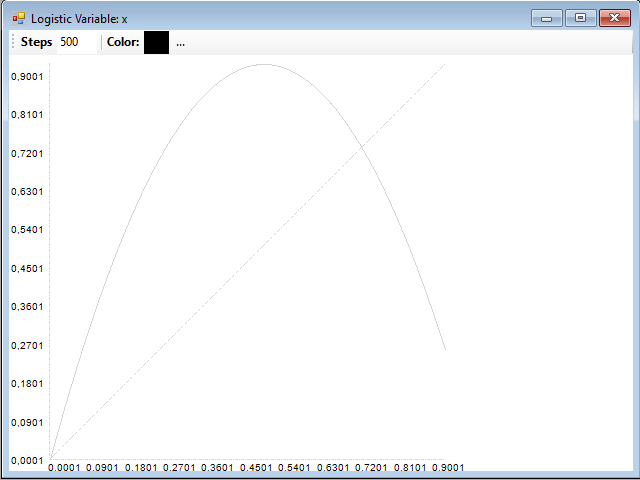
La parábola representa el valor de la función para los valores de Xn comprendidos entre el valor mínimo y máximo de la serie, dado un determinado valor de los parámetros. En el caso de GraphStudy, el procedimiento para obtener este gráfico es generar primero la serie temporal, con el botón Series, y, a continuación, usar el botón Web para generar el gráfico de recurrencia. En GraphStudy no se dibuja la parábola completa, sino solamente la parte de la misma en la que la función toma valores con los parámetros y valores iniciales dados.
En el gráfico, también trazamos una línea diagonal que representa los puntos en los que el eje de abcisas y ordenadas toman el mismo valor.
El eje horizontal corresponde con los valores de Xn, mientras que en el vertical representamos el valor de Xn+1. De esta manera, tomando cualquier punto Xn, podemos trazar una línea vertical hasta llegar al punto correspondiente a Xn+1, que se encuentra sobre la parábola.
A continuación, se traza una línea horizontal hasta la línea diagonal. La dirección de esta línea depende del lado de la parábola en la que nos encontremos. Con esto, nos situamos en el eje horizontal sobre la nueva Xn, y repetimos el proceso de trazar desde aquí una nueva línea vertical hasta el correspondiente punto Xn+1, sobre la parábola de nuevo.
Después de repetir este proceso numerosas veces, obtenemos una figura característica que nos indicará si la serie converge a un solo valor, presenta uno o más ciclos periódicos, o presenta trayectorias que parece que acabarán cubriendo todo el gráfico, lo que indica una dinámica caótica.
Para trazar un diagrama de recurrencia, primero debemos generar la serie con los parámetros y valor inicial deseados y, a continuación, pulsar con el botón izquierdo del ratón sobre el diagrama de recurrencia en el punto donde queremos empezar a trazar el diagrama. Podemos seleccionar el número de pasos que queremos realizar, escribiéndolo en el cuadro de texto Steps, y seleccionar el color con el que queremos trazar el gráfico.
Dándole al parámetro µ un valor dentro de la zona de dinámica estacionaria de la serie, por ejemplo 2,5, obtenemos el siguiente diagrama:
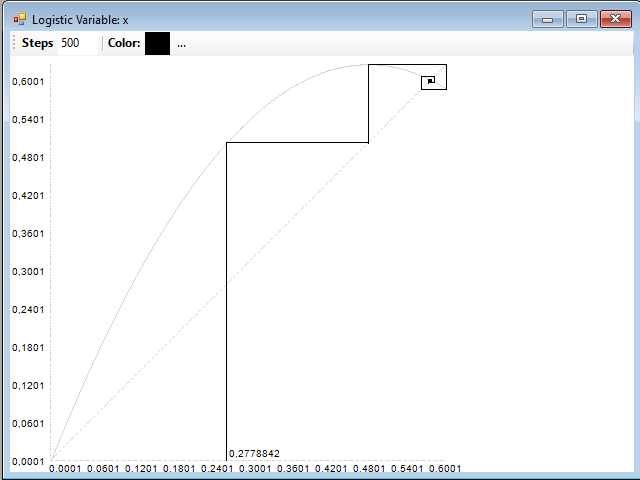
Donde puede comprobarse que la serie converge a un solo punto. Si ahora probamos un valor en la zona periódica, por ejemplo 3,3, obtenemos el siguiente diagrama:
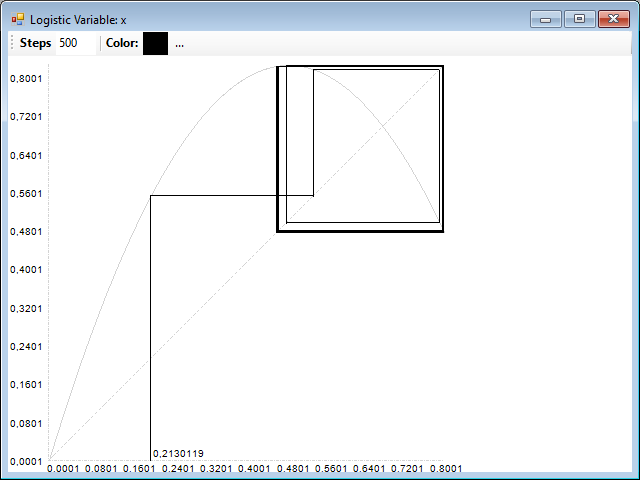
Donde puede verse que la serie acaba trazando un cuadrado, rebotando continuamente entre dos valores fijos.
Si ahora le damos a µ un valor en la zona de dinámica caótica, por ejemplo, 3,8, obtenemos el diagrama característico de esta dinámica, una trayectoria errática que prácticamente pasa por todos los puntos del gráfico:
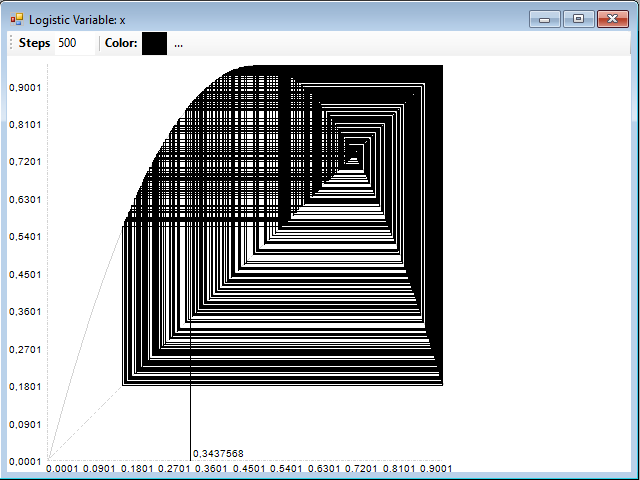
La aplicación triangular
Podemos ver otro ejemplo de serie que presenta diferentes comportamientos en función de sus parámetros, la aplicación triangular. Esta es la fórmula:
Xn+1 = µ(1-2abs(0,5-Xn))
Dando a µ valores en el intervalo (0,1). Si damos a µ un valor menor que 0,5, el sistema será estacionario, la serie converge a un único valor. Sin embargo, con valores superiores a 0,5, siempre presentará dinámica caótica. Este es el diagrama base de esta aplicación:
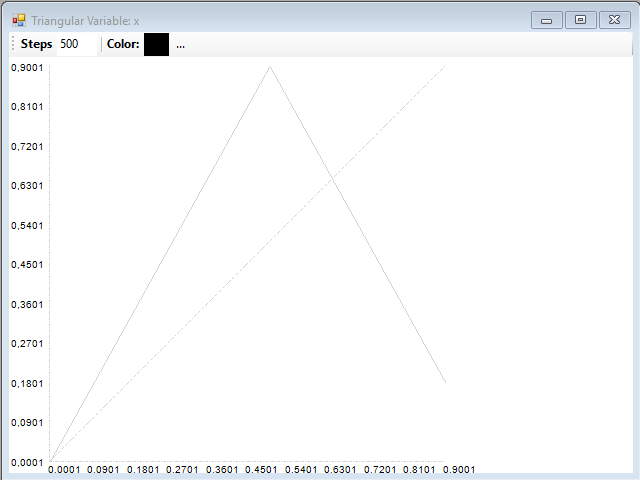
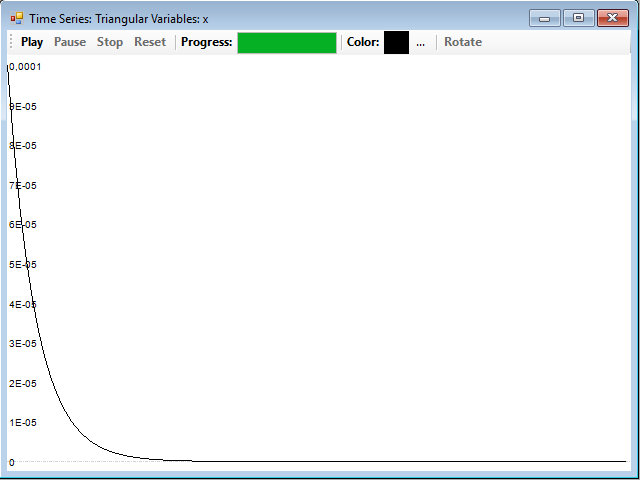
Con µ = 0,4 y un valor inicial para X de 0,0001, obtenemos una serie que converge a 0:
Y el correspondiente diagrama de recurrencia también lo indica:
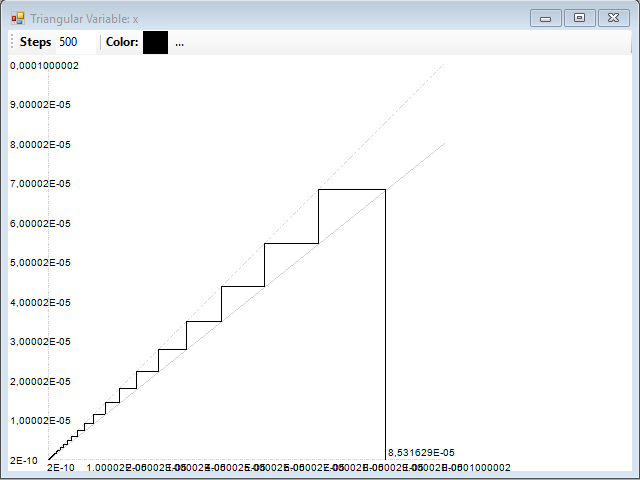
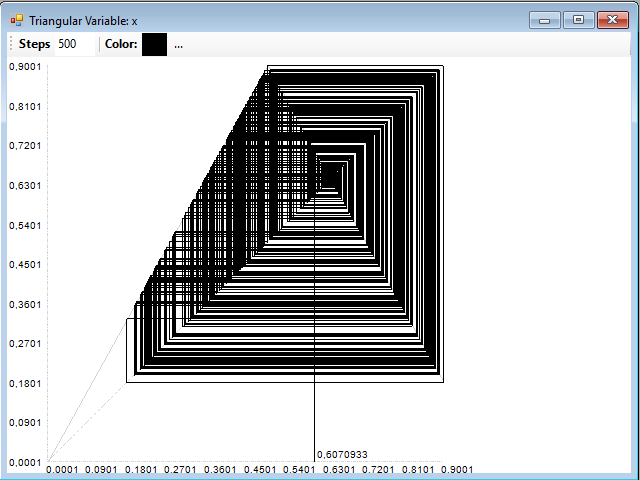
Sin embargo, con µ = 0,9, la cosa cambia bastante. Esta es la serie, con un valor inicial de 0,1:
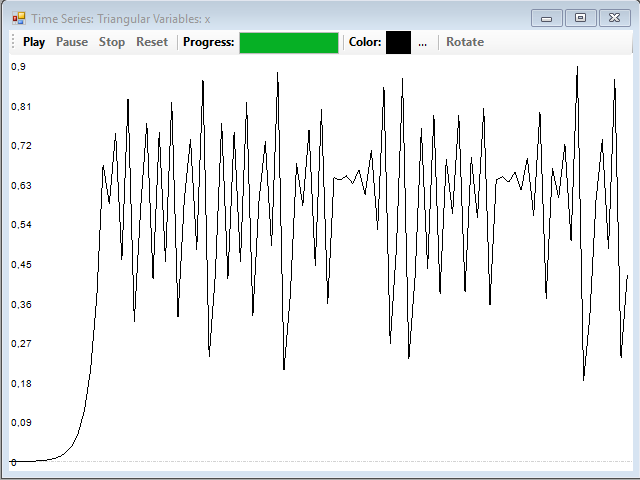
Y este es el diagrama de recurrencia correspondiente, que indica claramente la presencia de caos:
En el programa R, podemos dibujar estos gráficos de forma sencilla, por ejemplo, con el siguiente código:
fweb<-function(u,x) {
return (u*x*(1-x));
}
webdiagram<-function(p, steps=500) {
xn<-seq(0,1,length.out=1000);
xn1<-sapply(xn,fweb,u=p);
plot(xn,xn1,type='l',col="red");
lines(xn,xn,lty=4);
x0<-runif(1);
xn<-x0;
xn1<-0;
for (i in 1:steps) {
xf<-fweb(p, x0);
xn<-c(xn,x0);
xn1<-c(xn1,xf);
xn<-c(xn,xf);
xn1<-c(xn1,xf);
x0<-xf;
}
lines(xn,xn1);
}
Dentro de la función fweb podemos escribir las operaciones que van a generar la serie, el diagrama de recurrencia se dibuja con la función webdiagram. En este caso, estamos considerando funciones con un solo parámetro, pero es fácil modificar el código para utilizar un número arbitrario de parámetros.
Para terminar, os voy a recomendar un libro que es un clásico, donde podéis encontrar más sobre este y otros muchos temas: Fractals Everywhere, de Michael F. Barnsley.
El próximo artículo de la serie tratará sobre diagramas de fases y atractores.









