Dibujar fractales con Sistemas de Funciones Iteradas (IFS)
Los sistemas de funciones iteradas (SFI por sus siglas en inglés) son una herramienta matemática sencilla para construir conjuntos fractales por medio de un conjunto de aplicaciones afines contractivas. Este método fue desarrollado por M.F. Barnsley en 1985. En concreto, resulta de utilidad para obtener un fractal autosemejante a base de aplicar de forma iterativa el sistema de funciones a un conjunto cualquiera, hasta llegar a una buena aproximación del fractal que constituye el atractor del sistema.
Los SFI sirven también de base para algunos métodos de compresión de datos, sobre todo imágenes, pues permiten obtener buenas aproximaciones de objetos del mundo real. En lugar de almacenar todos los datos de las imágenes, lo que almacenamos en su lugar son los coeficientes de las funciones de los distintos sistemas utilizados para aproximar la imagen, que luego es reconstruida a partir de ellos.
En este artículo voy a utilizar una aplicación para mostrar el funcionamiento de este método, con la que se pueden definir sistemas de funciones y obtener imágenes de las fractales generadas por ellos. En este enlace puedes descargar el código fuente y el ejecutable del proyecto IFSDrawer, escrito en CSharp con Visual Studio 2015.
Aplicaciones afines contractivas
Voy a explicar un poco que es eso de las aplicaciones afines contractivas. Los ejemplos que voy a usar son para un espacio de dos dimensiones, un plano, pero pueden extenderse a espacios de cualquier dimensión.
Una aplicación afín F sobre un punto (x, y) del plano, se puede representar de la siguiente manera:
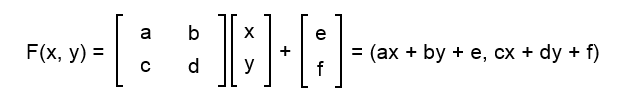
Los coeficientes e y f tienen una función evidente, la de desplazar la coordenada x y la coordenada y. Con los otros cuatro coeficientes, podemos realizar diferentes operaciones, cuyo sentido se ve mejor si imaginamos que estamos tratando los puntos de una determinada figura del plano.
Si dejamos a cero los coeficientes b y c, lo que hacemos es multiplicar las coordenadas x e y de los puntos por el valor de los coeficientes a y d, lo que hará que la figura se expanda o se contraiga en cada uno de los dos ejes.
También podemos crear una simetría respecto de los ejes horizontal y vertical haciendo que uno o los dos coeficientes sean negativos.
Si dejamos a cero los coeficientes a y d, podemos intercambiar, además de multiplicar por el valor de los coeficientes b y c, las coordenadas horizontales y las verticales.
También podemos girar la figura un ángulo ϕ dando el siguiente valor a los coeficientes: a=cosϕ, b=-sinϕ, c=sinϕ y d=cosϕ.
Podemos componer varios de estos movimientos obteniendo el producto de las matrices correspondientes a cada uno de ellos. Recordemos que, el resultado del producto de dos matrices A y A’ de 2x2, es otra matriz A’’ cuyos coeficientes valen: a’’=aa’+bc’, b’’=ab’+bd’, c’’=ca’+dc’ y d’’=cb’+dd’.
Una aplicación afín es contractiva si los coeficientes por los que multiplicamos son menores que la unidad y mayores que cero.
En .NET framework es muy fácil realizar transformaciones afines utilizando la clase Matrix del espacio de nombres System.Drawing.Drawing2D.
Sistemas de funciones iteradas
Los sistemas de funciones iteradas son conjuntos de n transformaciones afines contractivas. Normalmente se utilizan dos tipos de algoritmos, el algoritmo determinista y el algoritmo aleatorio.
El algoritmo determinista consiste en tomar un conjunto de puntos, que puede ser cualquier figura geométrica, y aplicarle cada una de las n transformaciones afines del sistema, con lo cual obtenemos n conjuntos de puntos transformados. A cada uno de ellos le volvemos a aplicar cada una de las n funciones, obteniendo n2 nuevos conjuntos de puntos.
Continuamos de esta manera iterando sobre los resultados, hasta que la unión de todos los conjuntos obtenidos en la última iteración se va aproximando a la figura que constituye el atractor del sistema. A este atractor llegaremos siempre, independientemente de la forma conjunto de partida. Cada IFS tiene un atractor característico, que será un fractal autosemejante, ya que está construido a base de copias de sí mismo, cada vez más pequeñas. Normalmente no hacen falta muchas iteraciones para obtener dicho conjunto fractal.
El algoritmo aleatorio es similar, pero en lugar de aplicar las funciones a un conjunto de puntos, las aplicamos sobre un único punto, que vamos dibujando. A cada una de las transformaciones del sistema le asignamos un valor de probabilidad, teniendo en cuenta que la suma total de los valores de probabilidad de las funciones debe valer 1. En cada iteración del algoritmo, seleccionamos una de las transformaciones con probabilidad p. Esto es muy sencillo de hacer, simplemente se obtiene un valor aleatorio entre 0 y 1, por ejemplo con la clase Random, y se van sumando una por una las probabilidades de cada función, hasta que el resultado sea mayor que el número aleatorio obtenido. Esa será la función seleccionada.
Los primeros puntos de la serie se descartan. Porque normalmente están muy alejados del atractor, el resto se van dibujando hasta obtener el dibujo del fractal correspondiente, normalmente después de un número de iteraciones entre 1000 y 5000.
Aplicación IFSDrawer
Vamos a ver ahora la aplicación que he preparado para ilustrar todo esto. Se trata de un formulario que tiene el siguiente aspecto:
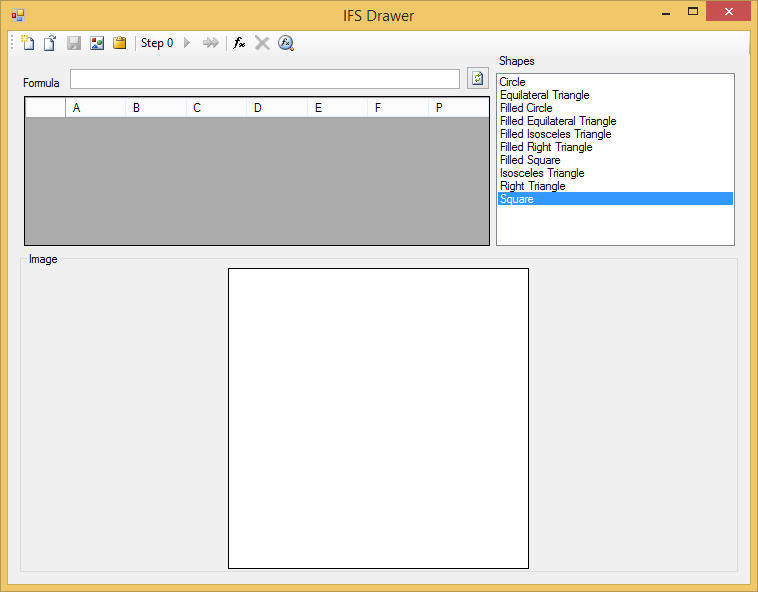
En la lista desplegable Shapes, a la derecha, se pueden seleccionar diferentes polígonos de partida para iterar el algoritmo determinista. En la parte inferior veremos cómo se va dibujando el atractor. Los coeficientes de las diferentes transformaciones los escribiremos en el DataGridView de la izquierda, que es un DataGridView con soporte para fórmulas del que ya he hablado en otro artículo.
Las fórmulas se pueden escribir en el cuadro de texto que hay sobre el grid y con el botón que hay a su derecha, se pueden compilar y asignar a las celdas seleccionadas. Estas fórmulas pueden ser de utilidad de cara a no tener que utilizar la calculadora para calcular los valores a escribir en cada uno de los coeficientes. Podéis consultar el artículo sobre este control sobre la sintaxis de las fórmulas. En esta aplicación he añadido al lenguaje las siguientes constantes, que también se pueden utilizar en las fórmulas:
- _pi y _e: Los valores correspondientes a los números pi y e.
- _rand: Devuelve un valor aleatorio entre 0 y 1.
- _width y _height: Son el ancho y el alto de la imagen mostrada en el formulario.
El primer botón, empezando por la izquierda, de la barra de herramientas es para borrar todo y empezar con un nuevo sistema de funciones. Con el segundo podemos abrir un fichero con un sistema de transformaciones que hayamos guardado previamente. El programa trabaja con dos formatos, csv y un formato binario propio de la aplicación, ifs. Las funciones definidas para el grid también se guardan en estos dos formatos junto con el resto de los datos.
En la carpeta Samples del proyecto IFSDrawer he dejado algunos ejemplos de sistemas. Si abres, por ejemplo, el archivo Sierpinski.ifs, verás lo siguiente:
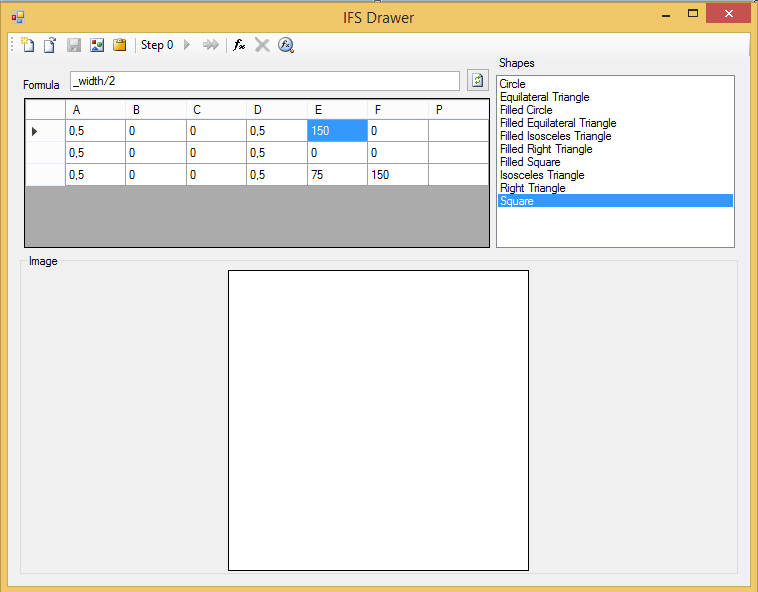
Existen tres transformaciones, cada una en una fila del grid, con sus coeficientes correspondientes. Como la columna P está vacía, se utilizará el algoritmo determinista para procesar el sistema.
El tercer botón de la barra de herramientas permite guardar el sistema de transformaciones en un archivo y el cuarto y el quinto se utilizan para guardar la imagen actual en un fichero o en el portapapeles, respectivamente.
Puedes añadir más funciones al sistema con el tercer botón, empezando por la derecha, o eliminar una de ellas con el segundo, después de haber seleccionado la fila correspondiente.
Antes de poder ejecutar el algoritmo, hay que procesar los valores del grid, para comprobar que estén completos y sean correctos. Para ello hay que utilizar el primer botón empezando por la derecha. También deberás usar este botón si has realizado algún cambio, antes de poder ver el resultado.
Una vez hecho esto, se activará uno de los botones centrales, con una flecha verde, y podremos comenzar a iterar el algoritmo, un paso cada vez, cada vez que pulsemos la flecha.
El resultado, después de 1, 3 y 8 iteraciones, es el siguiente:
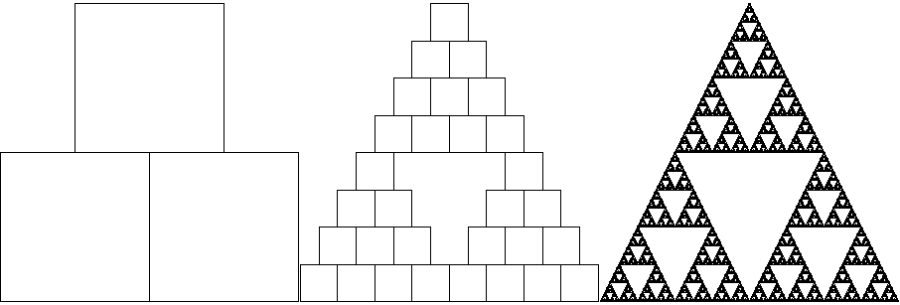
El conocido triángulo de Sierpinski. Podéis probar con cualquiera de las otras figuras, incluso con el círculo, que siempre obtendréis este triángulo, que es el atractor de este sistema de funciones.
Para ver un ejemplo de algoritmo aleatorio, puedes abrir el archivo de ejemplo Fern.ifs, que dibujará una hoja de helecho. Primero tendremos que pulsar el mismo botón que en ejemplo anterior para procesar las fórmulas. Podremos ver que, en la parte central, se activa esta vez un botón con dos flechas verdes, al lado del cual aparecen dos cuadros de texto. El primero es para el número de iteraciones. Hay que tener en cuenta que en este algoritmo no podemos ir paso a paso debido al gran número de veces que debe ejecutarse. También podemos indicar un factor de escala para la figura dibujada. El resultado es algo como esto:

En cuanto al código del programa, la clase Transformation se utiliza para almacenar los datos de cada transformación afín, en sus propiedades A, B, C, D, E, F y P, de tipo object genérico, que pueden contener valores de tipo double o fórmulas del tipo FormulaBase. El valor se recupera en formato double con las propiedades de solo lectura AValue, BValue, etc:
[Serializable]
public class Transformation
{
public Transformation()
{
}
public object A { get; set; }
public object B { get; set; }
...
public double AValue
{
get
{
if (A == null)
{
return double.NaN;
}
if (A is FormulaBase)
{
return (A as FormulaBase).Value;
}
return (double)A;
}
}
...
}
La clase está decorada con el atributo Serializable de manera que podemos guardarla en un archivo.
Las formas geométricas son todas descendientes de la clase base abstracta ShapeBase:
public abstract class ShapeBase
{
protected GraphicsPath _path;
protected bool _fill = false;
public ShapeBase()
{
}
public ShapeBase(ShapeBase clon, Transformation tr)
{
_path = clon._path.Clone() as GraphicsPath;
Transform(tr);
}
public abstract void SetInitialSize(SizeF sz);
public virtual ShapeBase Draw(Graphics gr, Transformation tr)
{
if (tr != null)
{
ShapeBase snw = GetType().GetConstructor(
new Type[] { typeof(ShapeBase),
tr.GetType() }).Invoke(new object[] { this,
tr }) as ShapeBase;
snw.Draw(gr);
return snw;
}
else
{
Draw(gr);
return this;
}
}
protected virtual void Transform(Transformation tr)
{
Matrix m = new Matrix((float)tr.AValue, (float)tr.BValue,
(float)tr.CValue, (float)tr.DValue,
(float)tr.EValue, (float)tr.FValue);
_path.Transform(m);
}
protected virtual void Draw(Graphics gr)
{
if (_path != null)
{
if (_fill)
{
gr.FillPath(Brushes.Black, _path);
}
else
{
gr.DrawPath(Pens.Black, _path);
}
}
}
}
La clase tiene una variable _path de tipo GraphicsPath, donde se definen las líneas y puntos con los que se dibuja. El método SetInitialSize se utiliza para inicializar la forma con un tamaño inicial determinado. A este método solo se llama una vez, al crear el objeto, con el tamaño total del área de dibujo. Cada una de las formas debe crear e inicializar el objeto GraphicsPath que le corresponde.
El constructor con parámetros se utiliza para crear una copia de una forma a la que se le aplica una transformación. La transformación se aplica con el método Transform, que simplemente crea un objeto de tipo Matrix y aplica la transformación al GraphicsPath con su método Transform.
La forma se dibuja llamando al método Draw, al que se le pasa el objeto Graphics donde se debe dibujar y una Transformation que se le debe aplicar. Si este segundo parámetro es null, la forma simplemente se dibuja sobre el Graphics, en caso contrario, se crea una copia a la que se le aplica la transformación, se dibuja esta y se devuelve como resultado del método.
Definir una forma cualquiera es muy sencillo, solo hay que implementar el método SetInitialSize y una versión de ToString para que el nombre de la forma aparezca en la lista. El formulario IFSForm se encarga, en el evento Load, de enumerar todas las clases del ensamblado que descienden de ShapeBase para añadirlas a la lista, por lo que no es necesario hacer nada más. Esta es, por ejemplo, la implementación de un cuadrado:
public class Square : ShapeBase
{
public Square()
: base()
{
}
public Square(ShapeBase clon, Transformation tr)
: base(clon, tr)
{
}
public override void SetInitialSize(SizeF sz)
{
_path = new GraphicsPath();
_path.AddRectangle(new RectangleF(0f, 0f,
Math.Min(sz.Width, sz.Height),
Math.Min(sz.Width, sz.Height)));
}
public override string ToString()
{
return "Square";
}
}
Y eso es todo. Para profundizar más en el tema, os puedo recomendar el libro Fractals Everywhere, de M.F. Barnsley, donde podéis encontrar un desarrollo matemático más riguroso de los SFI, y el clásico La geometría fractal de la naturaleza, de Benoit Mandelbrot.









