Reconocimiento de posturas con Kinect I
Una de las posibilidades más interesantes que nos ofrece el sensor Kinect de Microsoft es la detección de cuerpos humanos, que nos permite desarrollar aplicaciones basadas en las distintas posturas que adopta el usuario o que son manejadas a distancia utilizando las posiciones de las manos. Para ello, proporciona una serie de puntos que representan las diferentes articulaciones del cuerpo.
Dependiendo del modelo de sensor tendremos más o menos puntos del cuerpo. La versión más básica es la que corresponde a la Xbox 360. Con el sensor de la Xbox One se añade la punta de los dedos pulgar e índice de las manos y un punto extra en el centro de la columna vertebral. Estas son las diferentes articulaciones y sus nombres:
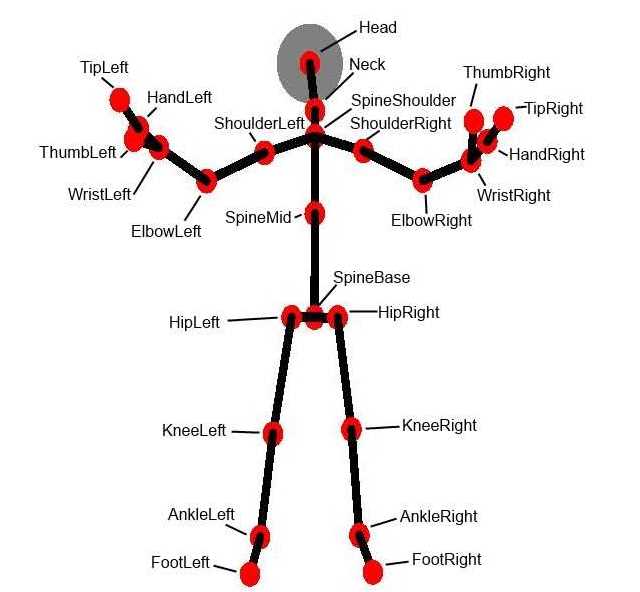
Cada articulación está representada básicamente por tres coordenadas X, Y y Z, estando el punto (0,0,0) situado en el sensor. También se indica para cada una de ellas la precisión de su medida: si está completamente determinada, si se trata de una posición inferida o si no se ha podido determinar. Como dato extra tenemos un indicador que nos dice si cada mano está abierta, cerrada o en una posición llamada lasso, con los dedos índice, corazón y pulgar extendidos y el resto de la mano cerrada.
Con todo esto puede parecer sencillo determinar la posición del cuerpo, pero la cosa tiene su complicación, y hay que hacer algo de trabajo matemático para simplificar la tarea. Para empezar, debemos dividir el problema en una serie de problemas más sencillos. Aunque el número de posiciones diferentes que puede adoptar el cuerpo son bastante numerosas, si nos fijamos en diferentes partes del mismo por separado veremos que los movimientos están bastante limitados.
En esta serie de artículos tomaremos como ejemplo el antebrazo. Si mantenemos inmóvil el resto del brazo, veremos que el único movimiento que puede hacer es una rotación limitada con el eje situado en el codo: desde una posición de unos 180 grados, con todo el brazo extendido, hasta poco menos de 45 si lo doblamos completamente.
Pero como el brazo puede girar libremente alrededor del hombro, debemos recurrir a algún tipo de proceso de normalización de la posición que nos facilite el cálculo de su posición basándonos solo en este ángulo.
Para ello, tomaremos solo los huesos del antebrazo y del brazo, representados por los puntos que corresponden a la muñeca, el codo y el hombro. El primer paso consistirá en hacer que el codo sea el origen de coordenadas, es decir, el punto (0,0,0). Esto se consigue fácilmente restando a cada uno de estos puntos las coordenadas del punto que representa el codo.
Una vez situado el origen de coordenadas, el siguiente paso es colocar los dos huesos en un mismo plano, por ejemplo el YZ. Para ello, debemos recurrir a la rotación de vectores en un espacio tridimensional. Tenemos dos vectores que rotar, el antebrazo, que va desde el codo hasta la muñeca, y el brazo, que va desde el codo hasta el hombro. Como el codo está en el origen de coordenadas, podemos aplicar las ecuaciones estándar de rotación de un vector en el espacio alrededor de los ejes X, Y y Z:
Para rotar alrededor del eje X: (en dirección contraria a las agujas del reloj)
X’ = X
Y’ = X * cos(a) – Y * sin(a)
Z’ = Y * sin(a) + Z * cos(a)
Donde a es el ángulo que queremos rotar el vector.
Para rotar alrededor del eje Y:
X’ = X * cos(a) + Z * sin(a)
Y’ = Y
Z’ = -X * sin(a) + Z * cos(a)
Y para rotar alrededor del eje Z:
X’ = X * cos(a) + Y * sin(a)
Y’ = X * sin(a) + Y * cos(a)
Z’ = Z
El objetivo es situar el brazo de tal manera que tanto el punto del codo como el del hombro queden situados sobre el eje Z, mientras que el de la muñeca quede situado en el punto que le corresponda en el plano YZ, todo ello sin cambiar la posición relativa de los huesos. El proceso requiere tres pasos: en el primero, situamos el hueso del brazo en el plano YZ, rotando alrededor del eje Z, en el segundo, volcamos este hueso sobre el eje Z, rotando alrededor del eje X, por último, rotamos el hueso del antebrazo de nuevo alrededor del eje Z para situarlo en el plano YZ. Por supuesto, todas las rotaciones afectan a los tres puntos, de lo contrario deformaríamos la posición de los huesos. Este es el procedimiento en forma de dibujo:
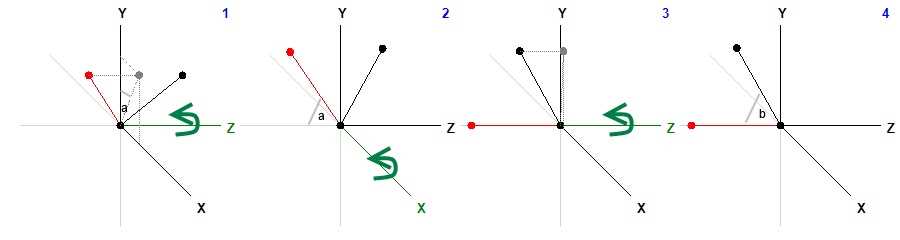
No hace falta calcular el ángulo que forma el vector con un eje para rotarlo, podemos calcular directamente el seno y el coseno. Como uno de los ejes lo utilizaremos solo para rotar el vector, usaremos la proyección de las coordenadas en los otros dos para calcular el ángulo de rotación. Empezaremos calculando la norma del vector, es decir, su longitud, para transformarlo en un vector de longitud unidad, dividiendo cada una de las coordenadas por la norma.
La norma se calcula de la siguiente manera:
||<X,Y>|| = SQRT(X2 + Y2)
Donde SQRT es la raíz cuadrada.
Una vez convertido el vector <X,Y> en unitario, para conocer el seno y el coseno del ángulo que forma con el eje X, por ejemplo, tomaremos como coseno el valor de la coordenada X, y como seno el de la coordenada Y. Para el ángulo con el eje Y basta tomar como coseno el valor de la coordenada Y y como seno el de la coordenada X.
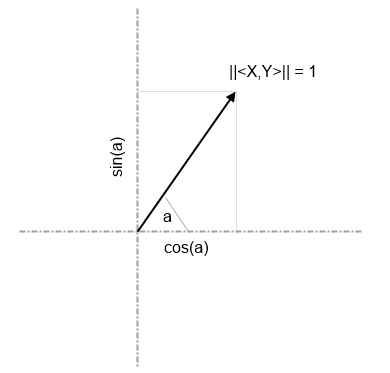
Este mismo procedimiento nos servirá para determinar finalmente el ángulo que forma el antebrazo con el eje Z. Pero para simplificar, en lugar del ángulo exacto dividiremos todo el posible círculo en sectores de varios grados de amplitud. En el código de ejemplo que acompaña a la serie de artículos he utilizado sectores de 18 grados, lo cual nos proporciona hasta 20 posiciones diferentes:
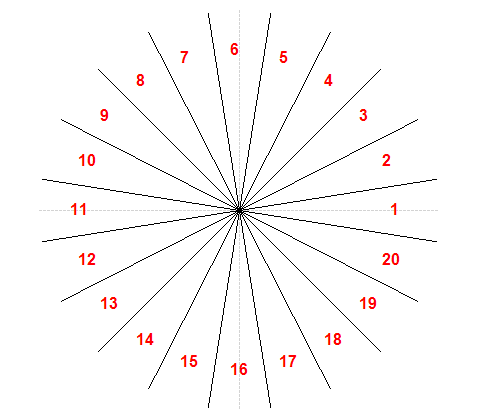
Por supuesto, con esto solo no bastaría para determinar posiciones complejas del cuerpo. El mismo procedimiento lo deberemos aplicar a otras partes del cuerpo y almacenar las posiciones relativas de cada una en un array o una cadena de texto. El antebrazo y la pantorrilla son las partes más fáciles, ya que solo pueden formar ángulo en un único plano. La pierna, el brazo o el torso pueden formar ángulos con más de un plano, por lo que en estos casos la normalización proporcionará más de un valor. Al final, como resultado lo que obtendremos es una serie de ángulos, pero en un número y un rango de valores menor que el de posibles coordenadas de todos los puntos de las articulaciones, lo que facilitará el trabajo de determinar la postura que está adoptando el cuerpo en cada momento.
En sucesivos artículos, proporcionaré ejemplos de código para llevar a cabo estas operaciones que os pueden servir de base para implementar vuestros propios algoritmos de normalización.









