Generación de números aleatorios
En muchas aplicaciones es necesario generar números aleatorios. Para esto, la .NET framework proporciona la clase Random, que permite generar valores pseudoaleatorios uniformemente distribuidos, lo que significa que todos los números tienen la misma probabilidad de aparecer en el resultado. Pero en algunos casos necesitamos generar valores aleatorios que sigan otros tipos diferentes de distribución. En este artículo vamos a ver cómo generar números aleatorios que sigan una distribución normal, con un sistema que podéis extender a cualquier tipo de distribución.
Existen varios sistemas diferentes para generar números según una distribución gaussiana, por ejemplo la transformación Box-Muller, del que existen diferentes variantes, como el método polar de Marsaglia. En este enlace podéis descargar ejemplos de código que utilizan el método Box-Muller.
Otro método, más eficiente, pero más complejo, es el algoritmo zigurat, en el que me he basado para desarrollar el código de este artículo. Básicamente consiste en dividir el área bajo una de las mitades de la distribución normal en rectángulos con la misma área y altura decreciente y seleccionar uno de ellos utilizando una distribución uniforme. A continuación, se multiplica la longitud de la base del rectángulo por un número aleatorio entre 0 y 1 y, si el resultado queda dentro de la parte del rectángulo que está contenido totalmente dentro de la curva de la distribución se devuelve este valor, o, en caso contrario, se sigue muestreando dentro del rectángulo hasta que se cumpla la condición. Un caso especial es el rectángulo de la base, ya que la distribución en las colas llega hasta el infinito, por lo que hay que implementar un procesamiento especial en caso de que este sea el rectángulo seleccionado.
Estos métodos se diseñaron en los años 60 del pasado siglo, cuando la memoria del ordenador era un recurso escaso y muy caro, por lo que utilizan el procesador realizando bucles hasta dar con el resultado o utilizan operaciones matemáticas que son costosas en tiempo de procesamiento. Actualmente, la memoria se ha abaratado muchísimo y cualquier ordenador tiene instalados varios gigabytes, por lo que podemos sustituir todos estos procedimientos por el uso de tablas de valores precalculados. Este es el método que sigo en el ejemplo de código que presento aquí. En este enlace podéis descargar el proyecto con el código de ejemplo para generar números aleatorios con distribución normal. El proyecto está desarrollado con Visual Studio 2013.
En lugar de dividir la superficie de la función de distribución en rectángulos con altura decreciente, dividiremos la altura de la curva en un número suficiente de puntos y almacenaremos el valor de la coordenada x correspondiente a cada uno de ellos. Esto es equivalente a construir una serie rectángulos cuya altura tiende a uno. La idea de construir rectángulos con altura decreciente tiene como objetivo que los rectángulos de la parte superior tengan más probabilidades de ser seleccionados al tener altura mayor, cuando se selecciona aleatoriamente un valor para la coordenada y, lo que vamos a hacer aquí es utilizar una segunda distribución normal, que proporcionará valores para seleccionar la coordenada y, produciendo el mismo efecto.
El problema de seleccionar valores en las colas de la distribución lo vamos a resolver limitando los valores devueltos a un intervalo de n distribuciones típicas, evitando así la posibilidad de llegar a valores infinitos.
Todos los cálculos necesarios se realizan en el constructor de la clase, por lo que la generación de los valores aleatorios no utiliza ningún bucle ni ningún cálculo complejo o costoso en tiempo de procesador.
Este es el constructor de la clase RandomNormal:
public RandomNormal(int resolution, int seed, double sdmax, double mean, double sd)
{
if (seed > 0)
{
r = new Random(seed);
}
else
{
r = new Random();
}
_mean = mean;
_sd = sd;
if (sdmax <= 0)
{
sdmax = 1;
}
_stack = new double[resolution];
ConstructNormal(_stack, resolution, sdmax, sd);
_sampler = new double[1000];
ConstructNormal(_sampler, 1000, 3, (double)resolution / 3);
}
En el parámetro resolution pasaremos el número de divisiones que vamos a realizar en el eje y, en seed podemos pasar una semilla para el generador de números aleatorios Random que utiliza la clase internamente, o 0 si no queremos ninguna. sdmax indicará el número de desviaciones típicas dentro de las cuales queremos generar resultados, y mean y sd son para la media y la desviación típica de la distribución.
La variable _stack es una array de valores de tipo double que contendrá las coordenadas x de la curva normal en cada uno de los puntos del eje de las y, mientras que _sampler se rellenará con los datos de la distribución normal para el muestreo, con un rango de tres desviaciones típicas y una desviación típica igual a la tercera parte de la resolución que hayamos indicado, de manera que devuelva valores en el rango del tamaño del array _stack. Los datos contenidos en estos arrays son para una distribución de media 0, la media real la añadiremos al generar los números aleatorios.
La función ConstructNormal es la que se encarga de calcular los datos de la distribución:
private void ConstructNormal(double[] data, int resolution, double sdmax, double sd)
{
double xmax = Math.Round(sd * sdmax, 10);
double gamma = Math.Round(sd * Math.Sqrt(2 * Math.PI), 10);
double ymax = Math.Round(1 / gamma, 10);
double ymin = Math.Round(ymax * Math.Exp(-0.5 * sdmax * sdmax), 10);
double yincr = Math.Round((ymax - ymin) / (double)resolution, 10);
data[0] = 0;
double y = ymax - yincr;
for (int layer = 1; layer < resolution; layer++)
{
double x = Math.Round(sd * Math.Sqrt(-2 * Math.Log(gamma * y)), 10);
data[layer] = x;
y -= yincr;
}
}
Para cada una de las divisiones del eje y, empezando por la más alta, calculamos la coordenada x correspondiente utilizando la función inversa de la función de distribución normal. El primer valor lo asignamos a la media directamente, pues siempre será 0, y empezamos a calcular a partir del siguiente nivel.
Por último, la generación de números aleatorios es extremadamente sencilla, realizándose en la función NextValue:
public double NextValue()
{
int slayer = r.Next(_sampler.Length);
int layer = (int)_sampler[slayer];
double mult = r.NextDouble();
double sgn = r.NextDouble() >= 0.5 ? 1 : -1;
return Math.Round(_mean + (mult * _stack[layer] * sgn), 10);
}
Primero seleccionamos un valor aleatoriamente de la normal de muestreo, que corresponderá con uno de los niveles de la distribución objetivo. El valor de este nivel lo multiplicamos por un valor aleatorio entre 0 y 1 y obtenemos un signo para seleccionar una de las dos mitades de la distribución. Finalmente, devolvemos el resultado centrado en la verdadera media de la distribución.
Ahora vamos a ver cómo usar la pequeña aplicación de ejemplo para generar números aleatorios y realizar tests de normalidad usando el programa R.
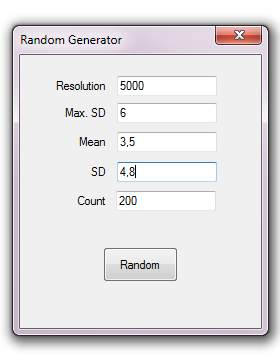
En primer lugar, introduciremos los parámetros apropiados, con cuyos valores podemos jugar hasta dar con los más apropiados para la distribución, que dependerán sobre todo de la desviación típica seleccionada.
Al pulsar el botón Random, se calcularán tantos valores como los indicados en la casilla Count, y se copiarán en el portapapeles en forma de un comando ejecutable en R que los asignará a la variable test.
A continuación, podemos ejecutar el comando en R pegándolo desde el portapapeles con Ctrl+V.
Empezaremos realizando un gráfico Q-Q plot para realizar un test visual:
qqnorm(test)
qqline(test)
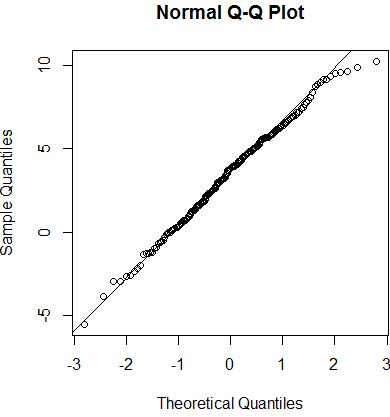
Podemos realizar un test de normalidad, como el test de Shapiro-Wilk:
shapiro.test(test)
Shapiro-Wilk normality test
data: test
W = 0.99358, p-value = 0.5397
El p-valor alto indica claramente que los datos proceden de una distribución normal, vamos a generar una secuencia con R de las mismas características para comparar:
rn<-rnorm(200, 3.5,4.8)
shapiro.test(rn)
Shapiro-Wilk normality test
data: rn
W = 0.99379, p-value = 0.5703
Como veis, nuestro algoritmo sale bastante bien parado en la comparación.
Este mismo sistema lo podemos aplicar a cualquier tipo de distribución de la cual deseemos obtener secuencias de números aleatorios, es rápido y bastante preciso, dadas las múltiples posibilidades de parametrización que tiene.









