Extensión I de WinRQA, estimación del retardo y la dimensión de inmersión

WinRQA es una aplicación dedicada a los mapas de recurrencia, una herramienta que se utiliza en el análisis de recurrencia de series temporales complejas. En este artículo voy a presentar la primera extensión de la aplicación, que consiste principalmente en una serie de ventanas de herramientas que nos permitirán realizar estimaciones sobre cuál puede ser el retardo más apropiado para tratar de reconstruir el espacio de fases del atractor del sistema y seleccionar la dimensión de inmersión correcta.

Para los detalles técnicos sobre este tipo de análisis, te puedo recomendar este sitio web dedicado por entero a los mapas de recurrencia, o este libro que trata sobre los mapas de recurrencia y su análisis.

En este enlace puedes descargar el ejecutable del programa WinRQA, y, en este otro, puedes descargar el código fuente del proyecto WinRQA, escrito en CSharp con Visual Studio 2013. Se trata de una aplicación para Windows, versión 7 o posterior.

En este otro enlace puedes encontrar el primer artículo de la serie sobre la aplicación WinRQA.

Las novedades introducidas en esta primera revisión de la aplicación son las siguientes:

• Posibilidad de trazar mapas de recurrencia de sistemas compuestos por más de una serie temporal.
• Posibilidad de crear mapas de recurrencia cruzados rectangulares, entre series de dimensiones diferentes.
• Herramienta para seleccionar el retardo utilizando la autocorrelación lineal de la serie.
• Herramienta para seleccionar el retardo utilizando la información mutua de la serie.
• Herramienta para seleccionar la dimensión de inmersión mediante la dimensión de correlación.

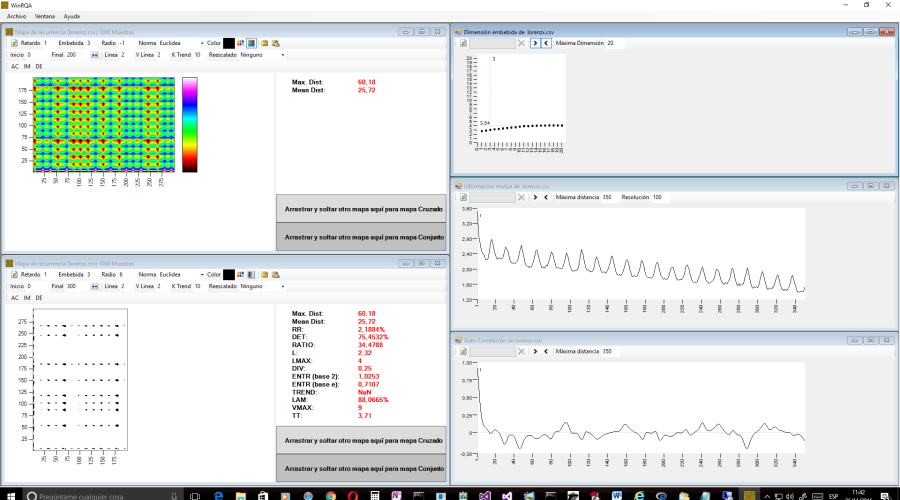
Mapas de recurrencia de sistemas de varias variables

Normalmente, los mapas de recurrencia se utilizan con series de valores que suponemos que proceden de sistemas con más de una dimensión. Sin embargo, podemos tener modelos teóricos de varias variables de los cuales disponemos de todos los datos. El programa ahora permite leer datos compuestos por más de una serie temporal, también en un archivo csv, con una columna por cada serie, separadas por el carácter punto y coma (;).

Estos sistemas se tratan como sistemas de dimensión fija, y no se puede modificar el valor del retardo ni la dimensión de inmersión, ya que no tenemos que reconstruir ningún espacio de fases, pues disponemos del modelo completo. Puede servir para realizar comparaciones entre este modelo completo y modelos simplificados formados por una sola serie de valores, por ejemplo.

En este enlace puedes descargar ejemplos de datos, el archivo lorenz3D.csv contiene las tres series de un atractor de Lorenz completo, mientras que lorenzx.csv, lorenzy.csv y lorenzz.csv contienen las series temporales correspondientes a las variables X, Y y Z respectivamente. Puedes ver que las series para la X y la Y son muy similares, pero diferentes de la Z, el sistema completo se reproduce mejor usando dos series, la Z y la X o la Y, según muestra el mapa de recurrencia conjunto, comparado con el mapa de recurrencia del sistema completo.

Mapas de recurrencia cruzados

En la versión inicial del programa, todos los mapas de recurrencia se dibujaban como un cuadrado. Sin embargo, los mapas de recurrencia cruzados pueden tener forma rectangular, según el tamaño de las ventanas de las series que estamos cruzando. En esta nueva versión se ha incluido esta funcionalidad, además de haberse corregido algunas incorrecciones en la construcción de este tipo de mapas.

Estimación del retardo más apropiado

Uno de los parámetros fundamentales para reconstruir correctamente el espacio de fases es el retardo a emplear para formar las dimensiones adicionales a partir de la serie original. Si se elige un retardo demasiado pequeño, el atractor reconstruido se encuentra demasiado comprimido, mientras que retardos excesivamente grandes producen atractores muy deformados debido a la des correlación de los valores de la serie.

Con la autocorrelación de los datos de la serie, podemos detectar relaciones lineales entre segmentos separados por un determinado periodo de tiempo. Para ello, simplemente basta con calcular la correlación lineal entre los valores de un segmento de la serie y otro segmento desplazado un tiempo t. Podemos dibujar una gráfica en la que representemos en el eje vertical el coeficiente de correlación, que tomará valores entre -1 y 1, y en el eje horizontal los diferentes intervalos temporales de separación.

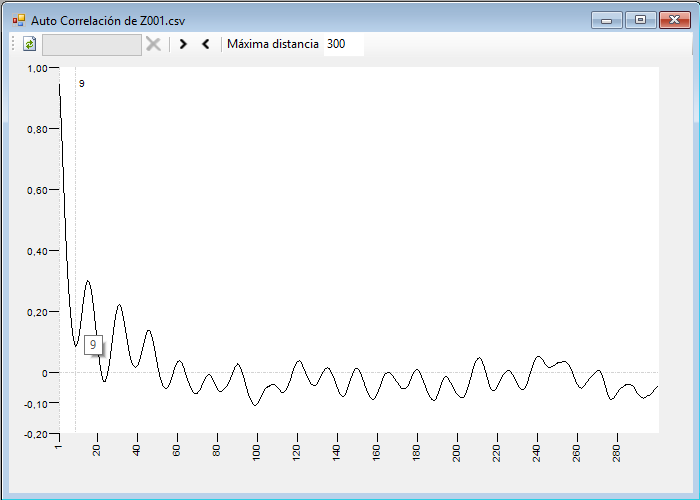
Podemos indicar la máxima distancia para la cual queremos calcular la autocorrelación de la serie. Con los botones podemos limitar los cálculos de manera que se tomen valore desde el inicio y/o hasta el final de la ventana de la serie con la que estamos trazando el mapa de recurrencia actual. El botón se utiliza para realizar los cálculos y dibujar la gráfica. Estos cálculos se realizan con un proceso en segundo plano, de manera que la aplicación pueda seguir utilizándose en caso de que lleven un periodo largo de tiempo.

Pulsando con el botón izquierdo del ratón sobre la gráfica podemos cambiar el valor del retardo en la ventana principal donde se encuentra el mapa de recurrencia. Un criterio muy habitual es seleccionar el primer mínimo local de esta gráfica como retardo de referencia.

Otra medida de autocorrelación que podemos calcular es la información mutua. Se trata de una generalización de la autocorrelación que nos permite encontrar relaciones no lineales en los datos. Se trata de un enfoque probabilístico en el que relacionamos la probabilidad condicionada de que aparezcan dos valores determinados a la vez en la serie separados por un determinado intervalo de tiempo con la probabilidad de cada uno de los valores por separado, según la fórmula:

P(s(t), s(t + τ))log2(P(s(t), s(t + τ))/P(s(t))P(s(t + τ)))

Calculamos y sumamos este valor para todos los términos de la serie completa, o de la ventana seleccionada, y dibujamos la gráfica como en el caso anterior.

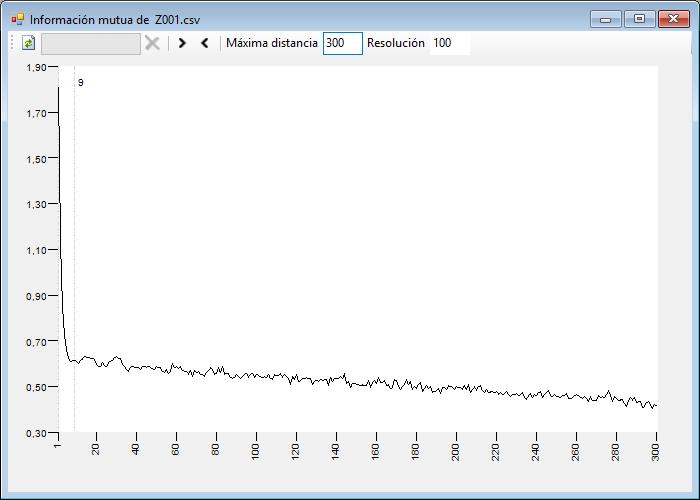
En esta ventana podemos indicar también un valor para la resolución que utilizaremos para construir el histograma de valores para calcular sus probabilidades. Este valor es la cantidad de intervalos en la que dividiremos el rango de valores de la serie de cara a discretizarlo.

Como en el caso anterior, también podemos utilizar como guía para seleccionar un valor apropiado para el retardo el primer mínimo local de esta gráfica.

Para utilizar estas herramientas, he añadido una nueva barra de herramientas a la ventana principal:

El botón AC mostrará la herramienta autocorrelación, e IM la herramienta información mutua.

Estimación de la dimensión de inmersión

En la nueva barra de herramientas existe un último botón, DE, que nos permite acceder a una herramienta que nos puede ayudar a estimar la dimensión más apropiada para construir el mapa de recurrencia.

Sabemos que, para reconstruir apropiadamente el espacio de fases del sistema, conservando sus propiedades topológicas, debemos utilizar una dimensión de inmersión con un valor de al menos 2d + 1, siendo d la dimensión del sistema en estudio.

Por otra parte, la dimensión de correlación se puede calcular de la siguiente manera:

ν = lim(r->0) Log(C(r)) / Log(r)

Donde r representa el radio que hemos seleccionado para el mapa de recurrencia y C(r) es la llamada integral de correlación, que no es más que el límite de la tasa de recurrencia del espacio de fases reconstruido usando ese radio r para determinar la vecindad. Se puede demostrar que este valor constituye una cota inferior de la verdadera dimensión del sistema.

Podemos graficar el valor de esta dimensión de correlación para diferentes valores de la dimensión de inmersión, de manera que podamos seleccionar dicha dimensión como aquella a partir de la cual ya no se producen cambios notables en la dimensión de correlación:

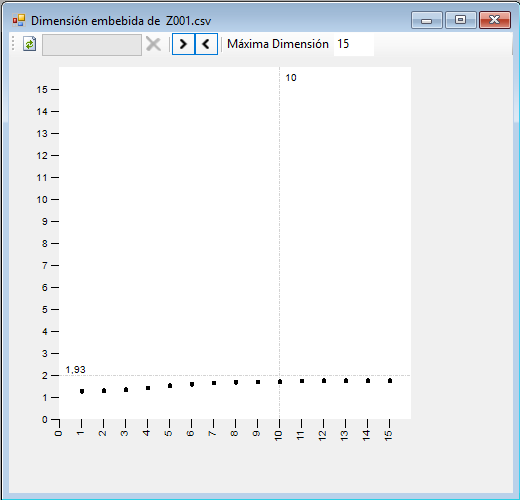
Podemos indicar la dimensión máxima que queremos explorar. Para cada uno de los valores de la dimensión, en el eje horizontal, podemos ver el valor de la dimensión de correlación, en el eje vertical, y una línea para la dimensión entera más cercana por encima de este valor.

En este enlace puedes encontrar el código fuente parcialmente comentado (en inglés) en CodeProject.

Puedes encontrar otra extensión del programa en el artículo extensión de WinRQA con series de medidas de recurrencia.