Series temporales complejas I, cuestiones básicas
Muchos de los conjuntos de datos con los que solemos trabajar se presentan en forma de series temporales. Una serie temporal se puede ver como la evolución de un sistema dinámico, caracterizado por una serie de variables y parámetros. Dependiendo del tipo de dinámica que presente el sistema, las series pueden ser estacionarias, periódicas, cuasiperiódicas, caóticas o aleatorias. En esta serie de artículos, me centraré en la caracterización de la dinámica caótica, que es la que presentan los sistemas complejos, utilizando métodos gráficos.
Si no tienes muy claro en qué consisten estos sistemas dinámicos, en este artículo puedes ver una breve introducción a los sistemas complejos.
Aunque para estudiar gráficamente estos modelos complejos se puede utilizar cualquier programa que nos permita generar gráficas y trabajar con funciones matemáticas, como el programa R, he desarrollado una aplicación auxiliar que permite generar las gráficas mediante un interfaz de usuario más simple y con el que se pueden exportar las series generadas a, o importarlas desde R de manera que podemos trabajar con ellas también con esta aplicación. En este enlace podéis descargar el ejecutable y el código fuente del proyecto GraphStudy, escrito en CSharp con Visual Studio 2013.
El programa GraphStudy
Para empezar, vamos a ver cómo empezar a trabajar con el programa GraphStudy. Se trata de una aplicación en la que se pueden escribir una o más ecuaciones y generar una serie de gráficas a partir de ellas. La gramática de estas expresiones está basada en la del artículo diseño de la gramática para un analizador de expresiones, se pueden utilizar los operadores de suma, diferencia, producto, división y exponenciación, y se han añadido las funciones seno (sin) y coseno (cos). Además se pueden utilizar las constantes e y pi, a las que se les dará automáticamente el valor correspondiente. Se pueden utilizar paréntesis para modificar la precedencia de los operadores.
Para escribir un nuevo sistema de ecuaciones, en el menú File seleccionaremos la opción New:
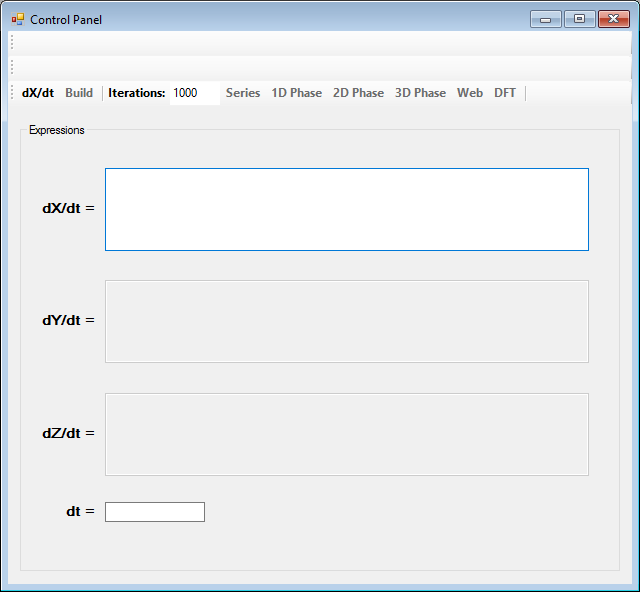
Con el botón dX/dt podemos seleccionar si queremos escribir un sistema de ecuaciones diferenciales, o bien un sistema de funciones iteradas:
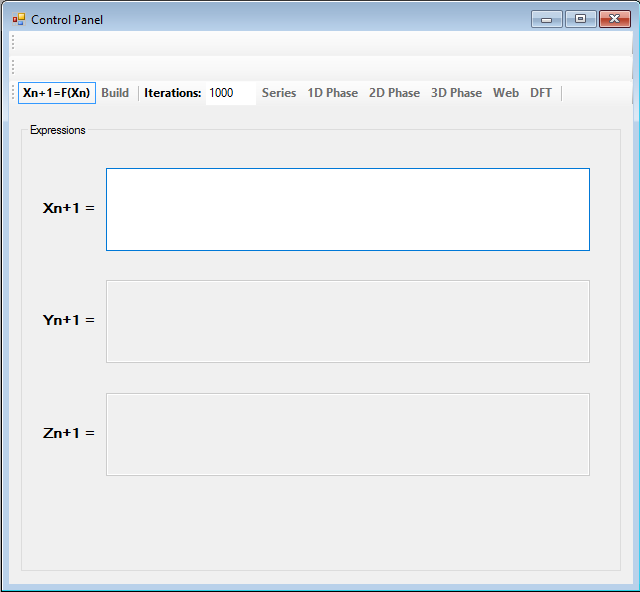
Podemos tener hasta tres variables, X, Y y Z. Cada vez que escribamos una ecuación para una de las variables, se activará la edición de la ecuación para la siguiente. De esta manera, podemos tener ecuaciones para X e Y, pero no para X y Z.
Una vez escritas las ecuaciones, se deben compilar utilizando el botón Build. Esto hará que aparezcan en las barras de herramientas las constantes y variables que hayamos utilizado en las ecuaciones y podamos darles valores para generar las series. Como variables, se pueden utilizar solamente X, Y y Z, como constantes, cualquier otra cadena de texto en número ilimitado.
En el cuadro de texto Iterations podemos definir el número de términos de la serie que queremos generar. Si utilizamos ecuaciones diferenciales, además habrá que definir el tamaño de la variación de la unidad de tiempo, en el cuadro de texto dt.
La ecuación logística
Uno de los modelos más habituales para estudiar la dinámica caótica en las series temporales es la ecuación logística, que, en su forma reducida, podemos expresar como:
Xn+1 = µXn(1-Xn)
Esta ecuación tan sencilla se utiliza en el estudio de dinámica de poblaciones. La variable X toma valores entre 0 y 1. La clave de esta ecuación está en el parámetro µ. En función de su valor, la serie generada presenta una dinámica estacionaria, periódica o caótica. La dinámica estacionaria se caracteriza por tender a un solo valor. Esta ecuación presenta una dinámica estacionaria cuando µ es menor que 3. A partir de 3, la función se vuelve periódica. Empieza oscilando entre dos valores y poco a poco, al aumentar µ, va duplicando el número de valores hasta llegar a 3,57, valor a partir del cual la dinámica se vuelve caótica, aparece sensibilidad a las condiciones iniciales y los siguientes valores de la serie comienzan a ser impredecibles. En este enlace podéis ver como explorar la curva logística con R, con GraphStudy simplemente escribiremos la ecuación como una función iterada y pulsaremos el botón Build para compilarla:
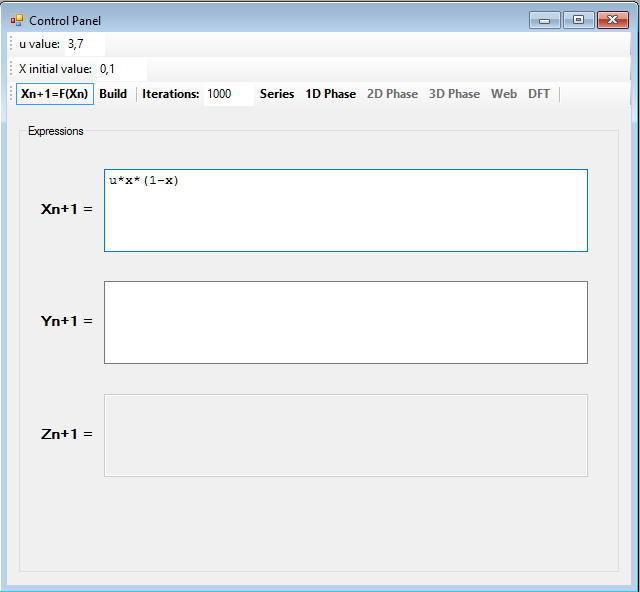
En la barra de herramientas aparecerá la constante u, a la que deberemos dar un valor entre 0 y 4, y la variable X, a la que daremos un valor inicial en el intervalo (0,1).
Una vez que tenemos definido un sistema de ecuaciones, en el menú File podemos utilizar las opciones Save y Save as… para guardarlo en un archivo y poder cargarlo más adelante utilizando la opción Open…
Con el botón Series podemos generar la serie correspondiente a los parámetros y los valores iniciales seleccionados. Por ejemplo, seleccionando un valor para µ de 2,5, que pertenece al dominio estacionario de la serie, y pulsando el botón Play de la ventana que aparece al pulsar el botón Series, obtenemos la siguiente serie:
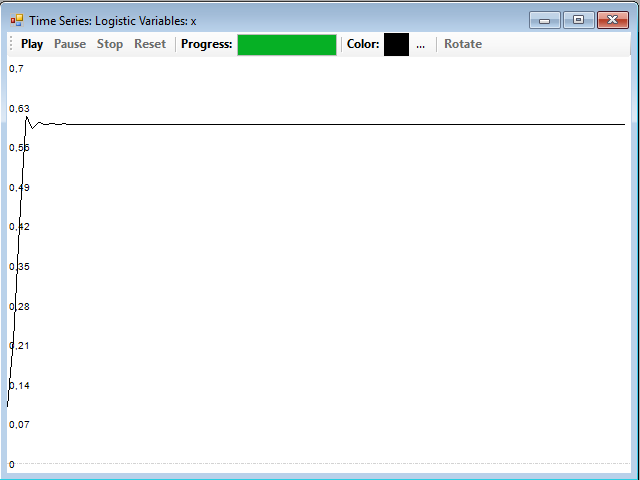
Si le damos a µ un valor en la zona periódica, por ejemplo 3,2, obtendremos una serie periódica:
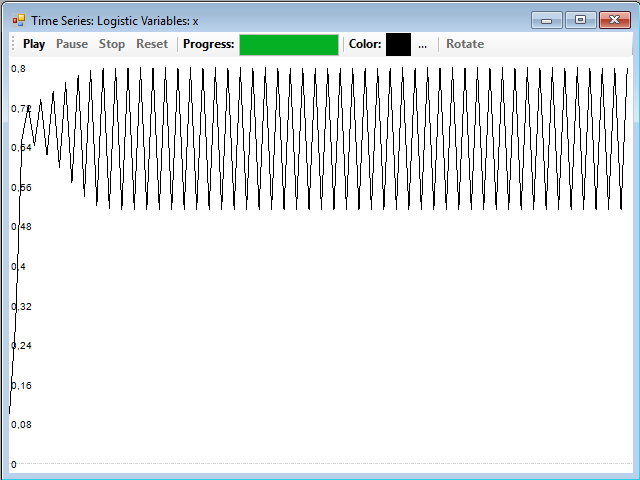
Como observación, fijaos en que existen una serie de puntos iniciales en los que el sistema está en una situación inestable hasta que alcanza la dinámica definitiva. Normalmente en estas series se descartan los N valores iniciales para evitar tener en cuenta en el estudio estos valores transitorios, que no son característicos de la serie y pueden distorsionar los resultados.
Si probamos con un valor de µ en la zona caótica, por ejemplo 3,7, obtenemos el siguiente resultado:
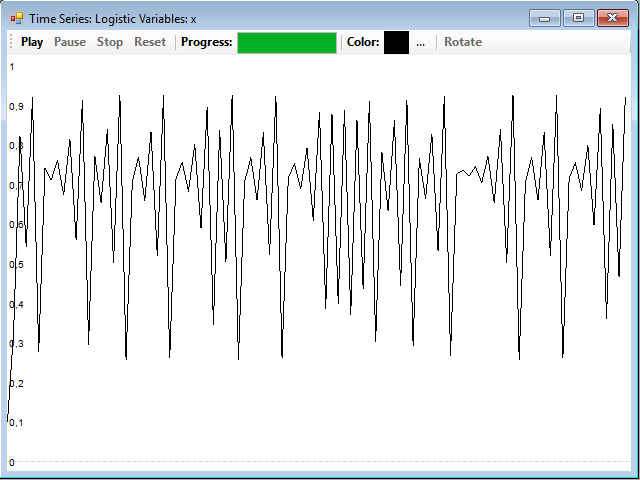
Si queremos constatar la sensibilidad de la serie a las condiciones iniciales, basta con abrir otra ventana con la misma ecuación y cambiar el valor inicial de la variable X. Generamos la serie, cambiamos el color de la gráfica en la ventana con la serie original, pulsando en el botón con los tres puntos, y arrastramos y soltamos la serie generada con el nuevo valor inicial sobre dicha ventana para superponerlas. En este ejemplo, podemos ver la diferencia entre la serie con un valor inicial de 0,1 y otro de 0,1001:
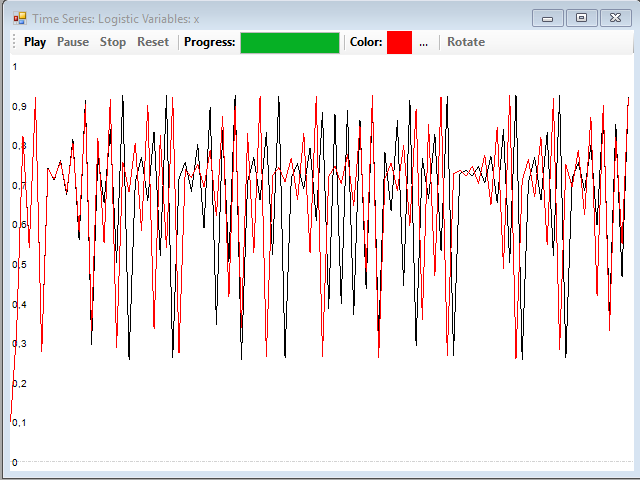
Vemos que, al principio, las dos series coinciden, pero pronto empiezan a tomar valores distintos y a divergir en dos series bastante diferentes. Estamos en presencia de una dinámica compleja.
En el siguiente artículo de la serie, hablaré sobre el uso de diagramas de recurrencia para detectar dinámica caótica.
Para terminar este artículo, os voy a recomendar un libro para empezar con este tema: El caos y las series de tiempo.









