Series temporales complejas V, autocorrelación y extensión de la dimensión
En este nuevo artículo de la serie sobre series temporales con dinámica compleja, voy a mostrar un procedimiento para reconstruir aproximadamente la información de un sistema dinámico de dos o más variables a partir de una única serie, es decir, de un conjunto de datos en una sola dimensión. Lo que haremos será obtener a partir de esta única serie una nueva serie para cada una de las dimensiones con las que pretendemos extender el modelo.
Como siempre, si quieres empezar la serie por el principio, este es el enlace al comienzo de la serie de artículos sobre caracterización gráfica de series temporales complejas. En este otro enlace os podéis descargar el ejecutable y el código fuente del proyecto GraphStudy, escrito en CSharp con Visual Studio 2013.
La idea en la que se basa la reconstrucción de nuevas dimensiones a partir de la serie unidimensional es la siguiente: suponemos que la serie de valores de la que disponemos corresponde a una de las variables de un sistema dinámico de mayor dimensión y que, por lo tanto, contiene información sobre el resto de las variables (dimensiones) del sistema, ya que todas ellas interaccionan entre sí.
Basándonos en el teorema de Whitney de la topología algebraica, consideramos que podemos reconstruir un atractor del sistema que, aunque no es el mismo que el del sistema original, sí es topológicamente equivalente, y conserva una estructura y propiedades similares. Para ello, construimos otra serie de puntos D-dimensionales, siendo D el número de dimensiones que queremos reconstruir, tomando para cada una de estas dimensiones un punto de la serie original tomado de una posición de la serie desplazada t elementos a partir del valor de la dimensión anterior.
Por ejemplo, para reconstruir tres dimensiones, tomaríamos para cada punto, los valores de la serie en Xi, Xi+t y Xi+2t, con lo que transformaríamos el punto Xi de una dimensión en el vector X3i, de tres dimensiones. Con estos puntos, podemos dibujar el diagrama de fases y visualizar el aspecto del supuesto atractor tridimensional reconstruido.
Hay que indicar que no todas las series nos van a permitir reconstruir un atractor de mayor dimensión. Es posible, por ejemplo, que la serie no contenga información sobre otras dimensiones, o que estas no existan. Se trata de una herramienta de análisis que nos permite estudiar si el sistema dinámico del que procede la serie temporal es caótico y presenta un atractor de dos o tres dimensiones, no de una receta mágica.
Autocorrelación e información mutua
La elección del desplazamiento t es determinante en la calidad del atractor reconstruido. Para seleccionar un valor adecuado, nos ayudaremos del estudio de la correlación de los valores de la serie con aquellos desplazados t elementos hacia delante.
Podemos utilizar la función de autocorrelación, que no es más que la correlación lineal entre los valores de la serie separados por un intervalo de d valores. Con la aplicación GraphStudy podemos graficar la correlación de la serie con diferentes intervalos. Para ello, se debe abrir un archivo csv o tsd (los archivos de datos propios de la aplicación) con la opción Open del menú File. Por ejemplo, el fichero Lorenz.tsd, con el atractor de Lorenz.

Con el botón L. Extend accedemos al formulario donde podemos dibujar la gráfica de la correlación lineal entre elementos de la serie a distintas distancias, antes comprobaremos que tenemos seleccionada la serie correspondiente a la variable X.
En el cuadro de texto Offset podemos definir el máximo desplazamiento al que queremos llegar en el cálculo de la correlación, por defecto vale 100, que es más que suficiente en la mayoría de los casos, ya que a distancias altas las series ya no presentan auto correlación prácticamente, pero como esta serie es bastante lenta y tienen 100000 valores, pondremos una distancia mayor, de 1000, por ejemplo.
Para calcular la gráfica de auto correlación, simplemente pulsa el botón Start.
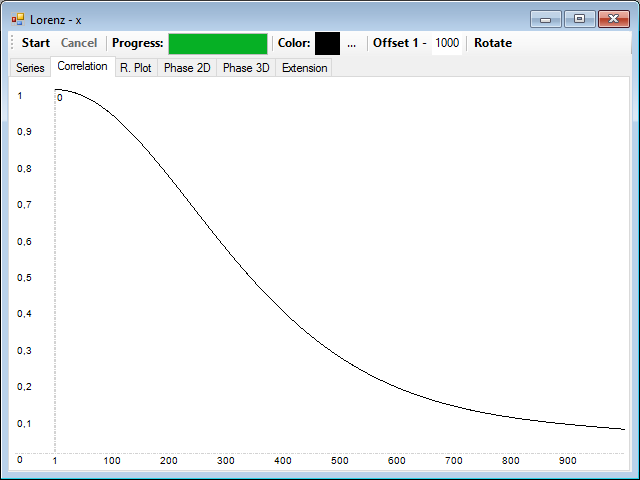
Vemos que la correlación va decayendo lentamente con la distancia.
La correlación lineal nos proporciona información sobre las relaciones lineales entre conjuntos de valores, pero se puede generalizar este concepto a las relaciones en los sistemas no lineales realizando el cálculo de la información mutua, basado en la teoría de la información.
Para ello necesitamos una distribución de probabilidades de los valores de la serie por separado y de los distintos pares de valores a una determinada distancia d. La información conjunta de los elementos Xi y Xi+d de la serie será:
I(Xi,Xi+d) = log2[P(Xi,Xi+d)/(P(Xi)P(Xi+d))]
Es decir, el logaritmo en base 2 del cociente entre la probabilidad (frecuencia) de que se presenten a la vez los dos valores a esa distancia y el producto de las probabilidades (frecuencias) de los valores por separado.
Si extendemos este cálculo a toda la serie, para cada distancia d tendremos la información mutua de la serie definida como:
I(d) = ΣP(Xi,Xi+d)I(Xi,Xi+d)
En GraphStudy, podemos realizar este cálculo de forma similar, con el botón P. Extend del panel de datos, ya lo utilizamos en el artículo anterior de la serie para obtener el histograma de frecuencias de los valores de la serie:
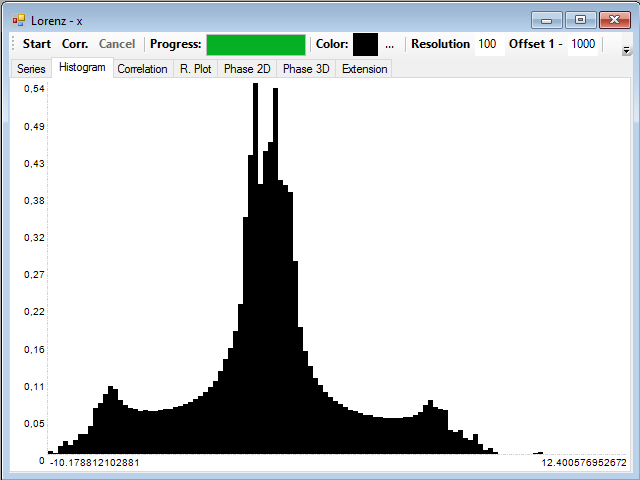
Para calcular el histograma se debe pulsar el botón Start. A continuación, con el botón Corr se calculará la información mutua de la serie y se dibujará su gráfica para las diferentes distancias, cuyo rango se puede modificar también en el cuadro de texto Offset:
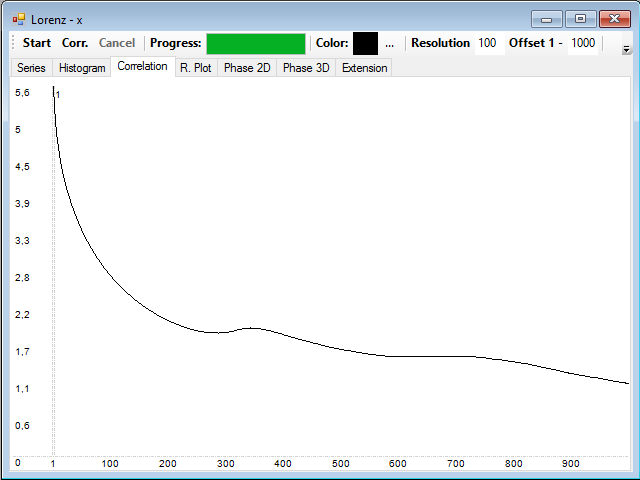
Podemos ver que la información mutua también decrece rápidamente con el tiempo.
Extensión de la dimensión
Una vez que tenemos la gráfica de correlación, cualquiera de las dos, podemos seleccionar sobre ella la distancia para reconstruir el atractor. En primer lugar, podemos ver el atractor completo, usando el botón 3D Phase del panel de datos y el botón Rotate para situarlo en una perspectiva adecuada:
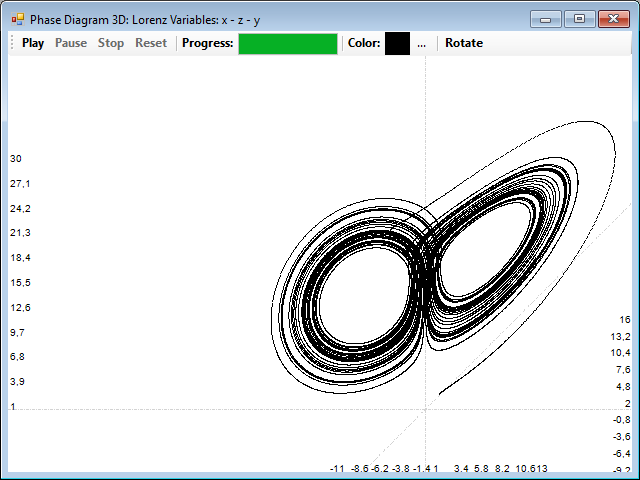
Si ahora pulsamos sobre una de las gráficas de correlación con el botón izquierdo del ratón, se marcará una distancia de correlación y podremos ver el correspondiente atractor reconstruido en dos dimensiones, pulsando sobre la pestaña Phase 2D, o en tres, seleccionando la pestaña Phase 3D, en este ejemplo, la distancia es de 22:
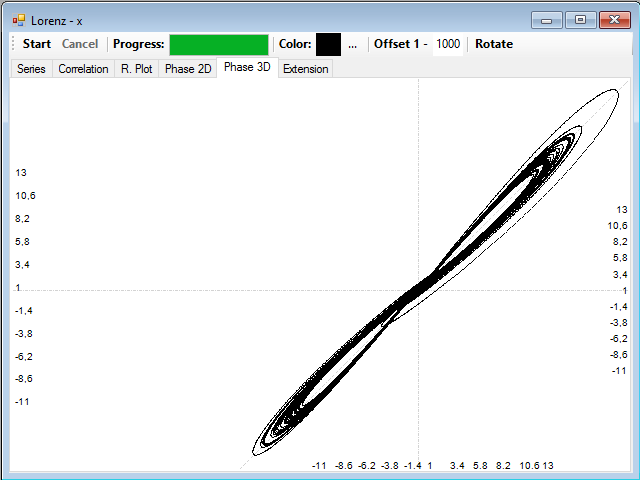
La distancia de correlación es demasiado corta y el atractor queda muy comprimido, si probamos ahora con una distancia larga de correlación, por ejemplo 500, el atractor queda muy distorsionado debido a la baja correlación que presentan los puntos:
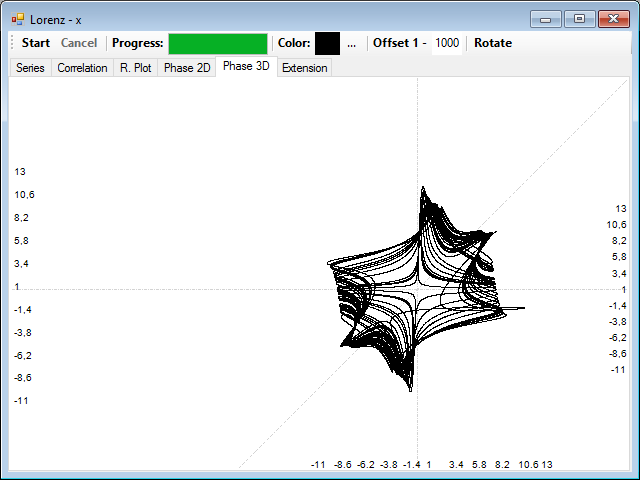
Seleccionando un valor intermedio, por ejemplo de unos 100, obtenemos una reconstrucción bastante buena del atractor completo:
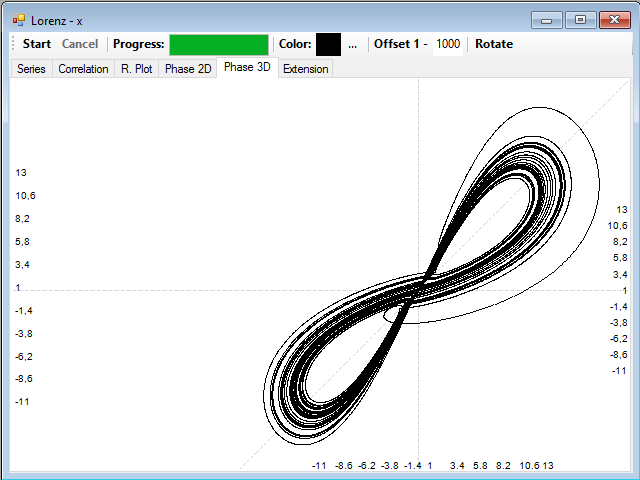
En la pestaña Extension se encuentran las series desplazadas para las otras dos variables Y y Z:
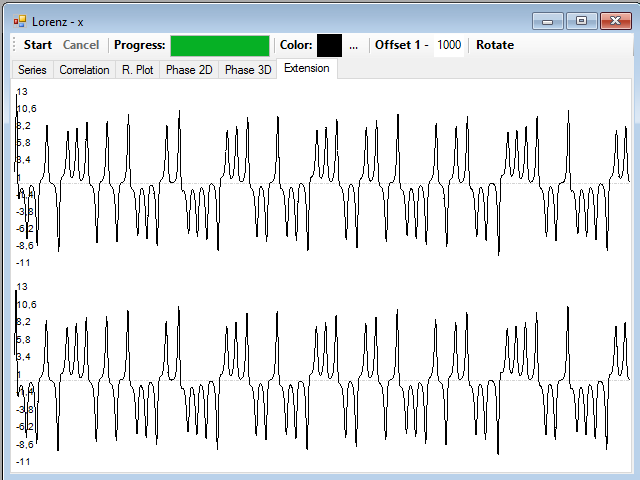
Podemos arrastrar y soltar una de ellas sobre una ventana donde se muestre la auténtica serie correspondiente a la variable para poder realizar una comparación visual, por ejemplo, esta es la serie reconstruida de la Y (en rojo) superpuesta con la original (en negro):
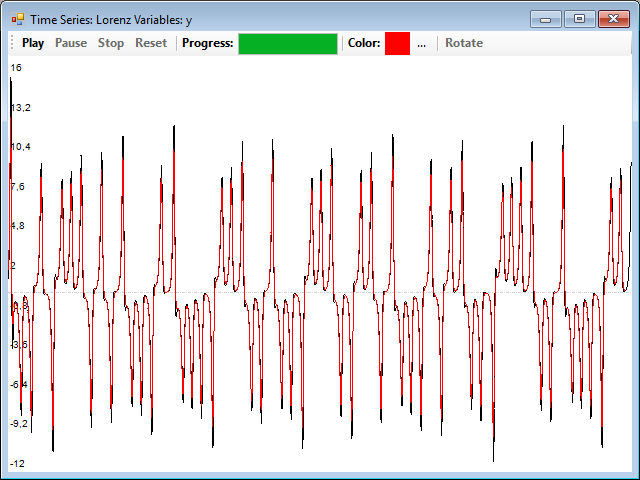
En realidad, la serie de las variables X e Y en el sistema de Lorenz son muy similares, por lo que este sistema se suele utilizar siempre como ejemplo de este procedimiento. Podéis encontrar otro ejemplo en el que las series ya no se parecen tanto y también se reconstruye bastante bien el atractor con una distancia de 1 si cargáis el archivo bi-logistic.tsd, reconstruyendo la serie a partir de la Y, la reconstrucción es bastante buena, pero la serie de la X original y reconstruida presentan mayores diferencias:
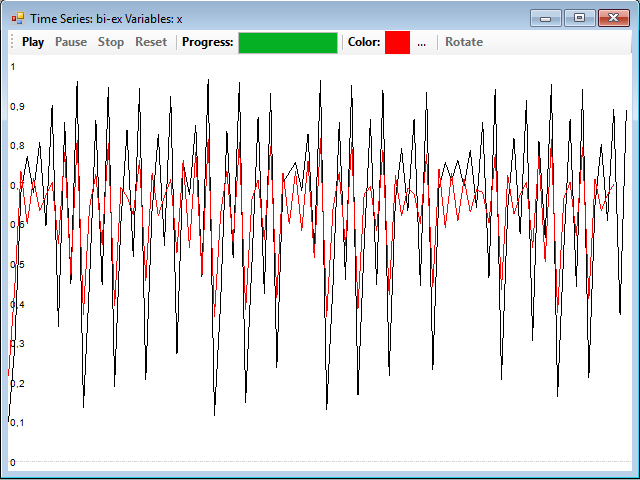
En el siguiente artículo voy a mostrar una herramienta sofisticada de análisis, los mapas de recurrencia.









