What is a complex system?
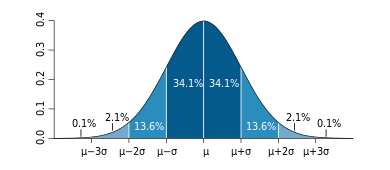
Usually, when you perform a data analysis, you suppose that they come from a normal distribution. In fact, you perform a battery of tests to verify that this assumption is met and, otherwise, you try to modify the data so that it is satisfied. This is because most analysis techniques only work properly on normally distributed data. But there are a number of systems that present a complex dynamics where is not valid to apply this hypothesis and wherein adjusting the data only leads to distortions that invalidate the results.
The study of these systems began in the field of physics, to address problems that resisted the classical approach, which considered the nature basically governed by deterministic laws. At the time the scientific and technical advances made possible to access to deeper levels of the structure of nature it began to be increasingly difficult to continue with this approach, emerging new lines of research and theories, such as chaos theory, catastrophe theory or synergetics.
From there, it has spread to other sciences, such as biology, with the study of population dynamics, trophic networks or the development of organisms, genetics, etc. Currently almost all disciplines count on techniques based on the study of complex systems. It is used increasingly in economics, sociology, and, since the explosion of big-data, in the data analytics in general, with applications such as machine learning algorithms, evolutionary algorithms and neural networks.

A dynamic system is basically a model that passes through different states depending on the time. We can find simple systems in which the transition from one state to another is completely determined and, given any state, we can predict the evolution of the system over time. These are called deterministic systems.
The thing thickens when we must begin to take into account the interactions between system elements. Even if each of them individually follows deterministic laws, the interaction between the components may make it impossible the system analysis with so few as three elements.
If we consider that in real systems that we analyze not only have many elements, but also there are multiple levels of aggregation at different scales, where interactions occur not only between elements of the same level, but these in turn interact with those in the other levels, we can realize the magnitude of the problem not only of predicting system behavior, but simply of the possibility of coming to understand its dynamics.
Consider, for example, the human societies, where we have individuals with different preferences, degrees of culture or ideologies, which in turn form different social groups and classes, occupy different geographical areas with particular needs and resources, create institutions at different levels, etc.
The problem when there are different levels of aggregation is that if, for example, we focus our viewpoint on one of the upper levels, taking enough data to make a detailed study of it, we have no choice but to consider the effects of lower levels, composed of an increasing number of items, grouping them and taking averages, losing a lot of information and, usually, underestimating or directly distorting these effects. The alternative is to consider an amount of data unmanageable in practice.
One of the characteristics of complex systems is the sensitivity to initial conditions, the famous butterfly effect, by which a small variation in the starting data of the system leads to completely different states. Therefore, in these systems, the measurement accuracy is critical, and can be reached to contradictory results simply by varying one decimal.
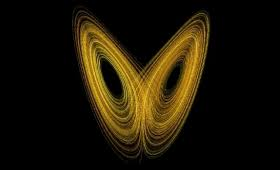
These systems can have many equilibrium states, which are states in which the system remains with a certain dynamics, being apparently robust to external interactions until suddenly a critical point is reached and it produces an abrupt change to a new equilibrium state, which is known as phase transition, as recently happened with the global economy in the 2008 crisis.
When analyzing normally distributed data, coming from a random system, the majority of events are clustered around the mean of the distribution. In the tails of the distribution there are highly improbable events, that we can discard without lose validity in the analysis, since the system does not thereby lose its randomness. However, in complex systems, highly improbable events can result in a phase change in the system, so that it is not advisable to overlook them. This gives an idea of the importance that may have correctly characterize the system we are studying, because, after a phase change, may lose their validity all the theories on which we rely to analyze the system.
Another characteristic that can be found in complex systems is scale invariance, namely the reproduction of similar structures at different levels of aggregation. This gives the system a fractal structure, which means that the geometry of the system has a fractional number of dimensions. For example, the curve of a polynomial function has only one dimension, but a fractal curve has a dimension between 1 and 2.

Finally, the aggregation and interaction of many elements in the complex systems, results in the appearance of emergent properties, which are properties of the system in a scale that cannot be explained simply by analyzing the properties of the elements that are below of that scale. Examples of emergent properties are the brightness of metals, and, one of the most important, the self-organization, observed for example in insect colonies or in the development of the animals from a single cell.
The study of dynamical systems is particularly interesting for the analysis of time series and their predictability. Complex systems are unpredictable by its nature from a certain period characteristic of each of them. Consider for example the weather forecasting, where accuracy is lost quickly in a few days from the current date. This is because these series have components in a very wide range of frequencies and is not always possible to collect data covering at least one full wavelength of all main frequencies.
In subsequent articles (as I go learning more about the matter), I will try to publish practical examples on how to characterize and work with these systems.
Here you have a couple of books on the sciences of complexity without mathematical developments with which you can explore much deeper into the subject:









