Más allá del caos, aleatoriedad
En este artículo voy a mostrar la manera en que, mediante un mismo proceso muy sencillo y totalmente determinista, podemos pasar desde un sistema estacionario a otro completamente aleatorio, pasando por dinámicas periódicas y caóticas. Para ello, voy a generar varias series temporales con estas características utilizando el programa R y varios paquetes que nos pueden ayudar en el análisis de las mismas.
En este enlace puedes descargar el código R , con una serie de funciones auxiliares que usaré a lo largo del mismo. En primer lugar, cargaremos este código:
source(“beyond-chaos.R”)
Dos de las funciones más simples y que nos permiten generar toda la gama de dinámicas simplemente variando un parámetro son la ecuación logística y la aplicación triangular. Se trata de funciones recursivas, donde cada término se obtiene a partir del anterior. La primera de ellas se expresa de la siguiente manera:
Xn+1 = µXn(1 - Xn)
Donde µ es un parámetro que toma valores en el intervalo (0, 4). La aplicación triangular se escribe como sigue:
Xn+1 = µ(1 – 2|0.5 - Xn|)
Aquí, el parámetro µ toma valores en el intervalo (0, 1).
Con el código fuente R podemos generar series temporales de las ecuaciones anteriores usando las siguientes funciones:
fLog<-function(u,length,initial) {
c<-1:(length+300);
c[1] <- initial;
for (i in 2:(length+300)) {
c[i]<-u*c[i-1]*(1-c[i-1]);
}
return(c[-(1:300)]);
}
fTriangular<-function(u,length,initial) {
c<-1:(length+300);
c[1] <- initial;
for (i in 2:(length+300)) {
c[i]<-u*(1-2*abs(0.5-c[i-1]));
}
return(c[-(1:300)]);
}
Ambas tienen los mismos parámetros, la longitud de la serie que queremos obtener (length), el valor inicial de la misma (initial) y el valor del parámetro µ. Descartamos los 300 primeros valores generados porque pueden ser valores transitorios hasta que la serie se estabilice en su dinámica final, de modo que así obtenemos datos sin distorsionar.
Para hacernos una idea del comportamiento de estos dos sistemas según vamos variando el parámetro, podemos dibujar un diagrama de Feigenbaum. Se trata de un diagrama en el cual en el eje de abcisas representamos los diferentes valores del parámetro µ y, para cada valor del parámetro, representamos en el eje de ordenadas todos los posibles valores que toma la serie con el parámetro dado. De esta forma podemos hacernos una idea del grado de complejidad a medida que incrementamos el valor del parámetro, las zonas con diferentes dinámicas y cada punto crítico donde se producen bifurcaciones. Para ello usaremos la siguiente función (adaptada de este artículo en R-bloggers):
feigenbaum<-function(start,end,step,fw) {
pu<-seq(start,end,by=step);
orbit<-sapply(pu,fw,initial=0.1,length=300);
r<-sort(rep(pu,300));
plot(r,orbit,pch=".");
}
Para la ecuación logística:
feigenbaum(2.5,4,0.003,fLog)
Obtenemos el siguiente diagrama de bifurcación:
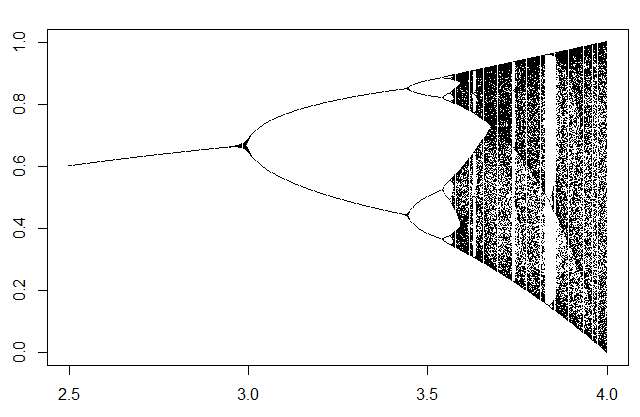
Donde podemos observar que la dinámica es estacionaria hasta llegar a un valor de 3 para µ, ya que la serie solo toma un único valor, y a partir de aquí se empiezan a producir bifurcaciones y la serie empieza a doblar el número de valores que toma, adoptando una dinámica periódica, hasta llegar a un punto en el que el número de valores se hace muy grande y entramos en la zona de dinámica caótica, algo más allá de 3.5.
Sobre la dinámica estacionaria y la periódica no voy a entrar en detalles, el único interés que tienen es que estas ecuaciones generan series temporales con estas dinámicas en ciertos rangos de valores del parámetro µ. La zona de dinámica caótica ya presenta propiedades interesantes que podemos estudiar.
Una de las propiedades principales de los sistemas caóticos es su sensibilidad a las condiciones iniciales. Esto hace que los fenómenos caóticos sean imposibles de reproducir o, lo que es lo mismo, de predecir su evolución. Veamos un ejemplo usando la aplicación triangular, con un valor del parámetro µ de 0.95, en la zona caótica, y un valor inicial de 0.1 comparado con otro de 0.1001:
plot(fTriangular(0.95,100,0.1),type="l")
lines(fTriangular(0.95,100,0.1001),col="red")

Como podéis ver, las dos series son totalmente diferentes al cabo de un cierto tiempo, generalmente muy corto (en este caso hemos eliminado los primeros 300 términos de la serie).
Por supuesto, al tratarse de un proceso totalmente determinista, si tenemos un valor exacto de la serie, podemos reproducirla con exactitud a partir del mismo, siempre que utilicemos la misma precisión que en la serie original, pero en la naturaleza normalmente las medidas que obtenemos no son nunca exactamente las mismas, por lo que los fenómenos caóticos son virtualmente irreproducibles.
Una herramienta gráfica interesante para determinar visualmente el grado de caoticidad de un sistema es el diagrama de recurrencia, que podemos dibujar con las siguientes funciones:
fWebLog<-function(u,x) {
return (u*x*(1-x));
}
fWebTriangular<-function(u,x) {
return (u*(1-2*abs(0.5-x)));
}
webDiagram<-function(p, steps=500, fw) {
xn<-seq(0,1,length.out=1000);
xn1<-sapply(xn,fw,u=p);
plot(xn,xn1,type='l',col="red");
lines(xn,xn,lty=4);
x0<-runif(1);
xn<-x0;
xn1<-0;
for (i in 1:steps) {
xf<-fw(p, x0);
xn<-c(xn,x0);
xn1<-c(xn1,xf);
xn<-c(xn,xf);
xn1<-c(xn1,xf);
x0<-xf;
}
lines(xn,xn1);
}
Las funciones fWebLog y fWebTriangular son funciones auxiliares para dibujar el diagrama de recurrencia de la ecuación logística o de la aplicación triangular. La función que dibuja el diagrama es webDiagram, a la que le pasamos el parámetro µ (en p), el número de pasos que queremos que dibuje (steps) y la función que queremos que utilice para trazar el diagrama (fw).
Para dibujar este diagrama, se traza la curva de la función en el rango de valores que tome la función dada (en nuestro caso siempre es (0, 1)) y una línea diagonal para la recta y = x. En el caso de la ecuación logística, la curva es una parábola, en el caso de la aplicación triangular, un triángulo. Se toma un valor cualquiera para empezar y se traza una línea recta desde el eje de abcisas hasta tocar la curva, desde este punto una línea horizontal hasta la recta y = x, y desde este punto de nuevo volvemos a trazar una vertical hasta la curva. Repetimos el proceso un número determinado de veces y obtenemos algo como esto:
Para la zona periódica de la ecuación logística:
webDiagram(3.4,fw=fWebLog)

La dinámica queda restringida a una zona bien delimitada. Sin embargo, en la zona caótica, por ejemplo de la aplicación triangular:
webDiagram(0.99,fw=fWebTriangular)

Podéis leer más sobre este tipo de diagramas en este otro artículo sobre diagramas de recurrencia.
Aunque la serie temporal sea en principio impredecible, podemos comprobar su carácter determinista utilizando, por ejemplo, redes neuronales para intentar aproximar la función a partir de una serie de valores. (En este enlace, puedes encontrar más sobre redes neuronales recurrentes y series de tiempo). Utilizaremos redes de Elman, por ejemplo con el paquete RSNNS:
require(RSNNS)
require(quantmod)
Lo primero que haremos será construir un conjunto de datos apropiado para su análisis con este tipo de redes, usando la función lagTS:
lagTS<-function(ts,lags) {
y<-as.zoo(ts);
for (l in 1:lags) {
y<-cbind(y,Lag(y,k=l));
}
return(na.omit(y));
}
En el dataframe que devuelve esta función, tenemos una primera columna con la serie original (ts), y una serie de columnas con valores de la serie desplazados un número determinado de términos (lags). Estas últimas se utilizarán para predecir los valores de la serie temporal original. Generamos la serie y usamos, por ejemplo, 10 series desplazadas para predecir:
tsl<-fLog(3.98,1000,0.2)
y<-lagTS(as.ts(tsl),10)
Usamos los 900 primeros valores para entrenar la red:
train<-1:900
inputs<-y[,2:11]
outputs<-y[,1]
fit<-elman(inputs[train],outputs[train],size=c(3,2),
learnFuncParams=c(0.1),maxit=1000)
Y tratamos de predecir los el resto de valores:
pred<-predict(fit,inputs[-train])
plot(as.vector(outputs[-train]),type="l")

lines(pred,col="red")

Al menos el siguiente valor de cada término de la serie está predicho con una muy buena aproximación. Si tratamos de predecir más términos veremos que los datos reales y predichos divergen rápidamente, pero podemos comparar lo que pasa si hacemos lo mismo con datos que en principio no son deterministas.
Podríamos simplemente generar una serie de números aleatorios con una función como por ejemplo rnorm o runi. Pero los números generados por este tipo de funciones suelen ser pseudoaleatorios, generados también mediante procesos deterministas, por lo que vamos a utilizar una serie verdaderamente aleatoria (en realidad, los resultados no van a ser muy diferentes, pero de esta manera nos aseguramos). Para esto, existe este generador de números realmente aleatorios, que utiliza datos procedentes del ruido atmosférico en lugar de generar números pseudoaleatorios.
En mi caso, he generado un archivo wav con ruido blanco con distribución uniforme. Para cargar un fichero de este tipo, podemos utilizar el paquete audio.
require(audio)
wv<-load.wave("soundfile.wav")
Con estos datos, podemos repetir lo anterior:
tsr<-(wv[1:1000] - min(wv[1:1000]))/(max(wv[1:1000])-min(wv[1:1000]))
y<-lagTS(as.ts(tsr),10)
inputs<-y[,2:11]
outputs<-y[,1]
fit<-elman(inputs[train],outputs[train],size=c(3,2),
learnFuncParams=c(0.1),maxit=1000)
pred<-predict(fit,inputs[-train])
plot(as.vector(outputs[-train]),type="l")
lines(pred,col="red")

Los valores se normalizan para que tomen valores entre 0 y 1 porque la red funciona mejor de esta manera, pero vemos que, en este caso, la red no ha podido aproximar la función que genera la serie. Aparentemente existe una diferencia notable entre los dos conjuntos de datos en cuanto a su complejidad, pero, ¿podemos llegar a hacer que estas funciones deterministas se lleguen a volver aleatorias?
En principio, con la ecuación logística, no podemos utilizar valores mayores que 4 para el parámetro µ, ya que a partir de este valor la serie se vuelve divergente. Parece que debemos detenernos en una dinámica caótica, pero, según el teorema central del límite, si sumamos varias variables con la misma distribución de probabilidades, obtendremos otra que tenderá a tener una distribución normal, podemos intentar promediar varias de estas series deterministas, iniciadas con diferentes valores para que sean todas diferentes, debido a su sensibilidad a las condiciones iniciales. Utilizaremos la siguiente función:
randFunc<-function(u1,u2,seed,length,count,fr) {
v<-fr(u1,count,seed);
x<-rep(0,length);
for(i in 1:count) {
x = x+fr(u2,length,v[i]);
}
return(x/count);
}
Los valores iniciales de las diferentes series los generaremos con otra serie de parámetro u1, generaremos count series de length valores usando la función fr, con el parámetro u2. El valor inicial para la serie de valores iniciales será seed. Las series generadas serán promediadas y se devolverá el resultado de esta operación.
Puede parecer que vamos a necesitar una gran cantidad de series para llegar a generar números realmente aleatorios, pero vamos a ver qué pasa si simplemente promediamos 5 series:
r5<-randFunc(3.9,3.99,0.2,1000,5,fLog)
Podemos realizar varias pruebas de normalidad:
shapiro.test(r5)
W = 0.99781, p-value = 0.2119
qqnorm(r5)
qqline(r5)

Podemos incluso recurrir a los mapas de recurrencia para intentar buscar rastros de determinismo en los datos pseudoaleatorios generados. Usemos el paquete crqa para generar un mapa de recurrencia de una serie caótica generad por la ecuación logística (en este enlace tenéis más información sobre esto, con la aplicación WinRQA para mapas de recurrencia):
Require(crqa)
tsl<-as.ts(fLog(3.98,198,0.2))
rqa<-crqa(tsl,tsl,delay=1,embed=1,rescale=0,radius=0.03,
normalize=0,mindiagline=2,minvertline=2,side="both")
Como no he encontrado ninguna función en el paquete para dibujar el mapa de recurrencia, podemos usar esta para hacerlo:
recurrencePlot<-function(rp) {
x<-rep(1:(dim(rp)[1]),dim(rp)[2])[as.vector(t(rp))==T];
y<-as.vector(sapply(1:(dim(rp)[2]),
rep,dim(rp)[1]))[as.vector(t(rp))==T];
plot(x,y,pch=".",pty="s",asp=1);
}
El mapa de recurrencia tiene este aspecto:
recurrencePlot(rqa$RP)

Se pueden observar claramente estructuras deterministas caracterizadas por líneas diagonales repartidas bastante ordenadamente por el gráfico. La medida RQA DET, o porcentaje de determinismo, es bastante alta:
rqa$DET
68.86727
Ahora podemos compararlo con el mapa de recurrencia de los datos realmente aleatorios obtenidos inicialmente:
tsl<-as.ts(wv[1:200])
rqa<-crqa(tsl,tsl,delay=1,embed=1,rescale=0,radius=0.05,
normalize=0,mindiagline=2,minvertline=2,side="both")
recurrencePlot(rqa$RP)

En este gráfico no se observan las estructuras deterministas, los puntos están aislados y el porcentaje de determinismo es mucho más bajo:
rqa$DET
9.7621
¿Y qué pasa con la serie aleatoria generada promediando series logísticas?, vamos a obtener también su mapa de recurrencia:
tsl<-as.ts(r5[1:200])
rqa<-crqa(tsl,tsl,delay=1,embed=1,rescale=0,radius=0.01,
normalize=0,mindiagline=2,minvertline=2,side="both")
recurrencePlot(rqa$RP)

Que podemos comprobar que no presenta tampoco rastros de estructuras deterministas. El porcentaje de determinismo es incluso mejor que en el caso de números realmente aleatorios:
rqa$DET
8.093995
Con esto hemos podido comprobar cómo puede surgir la aleatoriedad de procesos completamente deterministas, de manera que resulte indistinguible de una aleatoriedad real, suponiendo que realmente exista tal cosa.
En cualquier caso, este procedimiento no resulta óptimo para obtener números aleatorios, si estás interesado en ello, puedes leer este artículo sobre generación de números aleatorios con distribución normal.









