Maximizar o minimizar una función con el método Simplex

Existe un problema muy común en programación lineal que consiste en hallar los valores que hacen máxima o mínima una función lineal, dadas una serie de restricciones para dichos valores. Por ejemplo, puede tratarse de hallar una función de coste mínimo o de máxima producción. Para ello, existe un algoritmo desarrollado en 1947 por George Dantzig, llamado Simplex, que permite realizar dichos cálculos de una forma simple y efectiva.

La función de la cual queremos hallar el valor máximo o mínimo se llama función objetivo, y debe ser una función lineal de n variables, de la forma:

A1x1 + A2x2 + … + Anxn

Siendo los An cualquier número positivo o negativo.

Las restricciones son una cantidad cualquiera de condiciones, en forma de inecuaciones, que deben cumplir las variables para que la solución sea válida. Si se trata de maximizar la función, se deben expresar de la siguiente manera:

B1x1 + B2x2 + … + Bnxn <= C

Mientras que si lo que queremos es minimizarla, se deben escribir de la forma:

B1x1 + B2x2 + … + Bnxn >= C

Donde los Bn y C pueden ser cualquier número positivo, negativo o 0.

En este enlace podéis encontrar una explicación matemática del método Simplex, y en este otro podéis descargar el proyecto Simplex, con el código de ejemplo que acompaña a este artículo, escrito en CSharp con Visual Studio 2013.

El manejo de la aplicación es muy sencillo, basta con escribir la ecuación y sus restricciones, una en cada línea:

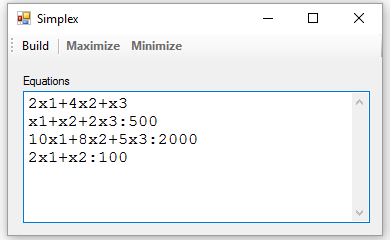
En la primera línea se debe escribir la función objetivo, y en las siguientes las restricciones, sin límite de número, sin dejar líneas en blanco. Como la inecuación cambia en función de que se trate de maximizar o minimizar la función, he sustituido los símbolos <= y >= por el signo :, que se tomará por uno de los anteriores, según corresponda.

Las variables pueden tener cualquier nombre que empiece por una letra, seguida de cualquier número de caracteres numéricos o alfabéticos, los números pueden tener decimales, y se puede usar el signo + o – para enlazar los términos de las ecuaciones. Si os interesa este tema, en este enlace podéis encontrar una serie de artículos sobre el diseño de la gramática para un analizador de expresiones, así como un ejemplo de implementación.

Una vez escritas las ecuaciones, se debe pulsar el botón Build para compilarlas, y, a continuación, ya se puede pulsar el botón Maximize o Minimize para que el programa proporcione los valores de las variables que hacen máxima o mínima la función con las restricciones dadas.

Dentro del programa, la clase que se encarga de realizar los cálculos es SimplexCalculator, y las clases que implementan el analizador de expresiones se encuentran en la carpeta Expressions. De estas, las clases que interesan son Expression, que implementa la función objetivo, y su clase derivada, ExConstraint, que implementa las restricciones. Estas clases tienen una propiedad Variables que proporciona una lista de objetos de la clase Variable, con las variables de la expresión.

El algoritmo consiste en construir una matriz con los coeficientes de la función objetivo y sus restricciones, además de los vectores de una base canónica de un espacio cuya dimensión depende del número de restricciones. Si, por ejemplo, el sistema de ecuaciones es el siguiente:

2x1 + 4x2 + x3
x1 + x2 + 2x3:500
10x1 + 8x2 + 5x3:2000
2x1 + x2 :100

Para maximizarla, la matriz se construye de la siguiente manera:

1 1 2 1 0 0 500
10 8 5 0 1 0 2000
2 1 0 0 0 1 100
2 4 1 0 0 0 0

En las tres primeras columnas están los coeficientes de las restricciones, en las primeras filas, y, en la última, los de la función objetivo. En las tres columnas siguientes la base canónica, en este caso de tres dimensiones, pues existen tres restricciones. En la última columna están las constantes que limitan los valores y el valor final de la función, en la última fila, que comienza con el valor 0.

El algoritmo está definido para maximizar la función, por lo que, si lo que queremos en minimizarla, la debemos reescribir de manera que se convierta en un problema de maximización, convirtiendo la función objetivo Z = AX, con las restricciones BX >= C, en la función Z = CY, con las restricciones BY <= A.

En el caso del sistema anterior, la matriz para la minimización se escribiría de la forma:

1 10 2 1 0 0 2
1 8 1 0 1 0 4
2 5 0 0 0 1 1
500 2000 100 0 0 0 0

Y se procedería con el mismo algoritmo que para la maximización.

En el caso de la clase SimplexCalculator, el constructor recibe como parámetros la función objetivo, en el parámetro target, la lista de las restricciones, en el parámetro constraints, y el parámetro maximize, que vale true cuando queremos maximizar la función, y false para minimizarla.

El constructor llama a la función CreateArray, que es la encargada de construir la matriz con los datos iniciales a partir de las expresiones.

La matriz de trabajo es un array de dos dimensiones de tipo double, la primera para las filas y la segunda para las columnas, que se almacena en la variable _simplex. Los coeficientes de las expresiones se obtienen con el método Coeficient de la clase Expression, al que se le pasa la variable de la que queremos extraer el coeficiente como parámetro.

También construimos un array en la variable _base que contendrá los índices de las columnas con los vectores de la base, que se irán moviendo de lugar a medida que se vayan realizando los cálculos. En otro array, en la variable _ccolumns, se almacenarán los índices de las columnas que usaremos para realizar los cálculos, que también se irán moviendo de lugar con cada paso del algoritmo, al ir realizando los cambios de base.

La lista de variables de la función objetivo se almacenan en una lista en la variable _lvars.

Una vez construido el objeto, para realizar los cálculos basta con llamar a la función Calculate, que devolverá el valor máximo o mínimo de la función y dará el valor final a las distintas variables de la función objetivo.

public double Calculate()
{
while (PerformStep()) ;
if (_maximize)
{
for (int ib = 0; ib < _base.Length; ib++)
{
if (_base[ib] < _lvar.Count)
{
_lvar[_base[ib]].Value =
_simplex[ib, _simplex.GetLength(1) - 1];
}
}
}
else
{
for (int iv = 0; iv < _lvar.Count; iv++)
{
_lvar[iv].Value =
-_simplex[_simplex.GetLength(0) - 1, iv + _ccolumns.Length];
}
}
return -Math.Round(_simplex[_simplex.GetLength(0) - 1,
_simplex.GetLength(1) - 1], cprecision);
}

Esta función llama repetidamente a otra función, PerformStep, que realiza cada uno de los pasos del algoritmo hasta que completa todo el proceso y devuelve false. A continuación, se asignan los valores a las diferentes variables. En el caso de una maximización, se obtendrán de la última columna del array _simplex, las posiciones contenidas en el array _base contendrán los índices de las variables a las que se debe asignar cada una de ellas.

En el caso de la minimización, los valores de las variables estarán en la última fila del array _simplex, en las posiciones donde se encontraban originalmente los vectores de la base.

El valor máximo o mínimo de la función se obtendrá de la posición correspondiente a la última fila y última columna del array _simplex.

La función PerformStep realiza cada uno de los pasos del algoritmo:

private bool PerformStep()
{
Point pivot = SelectPivot();
if ((pivot.X < 0) && (pivot.Y < 0))
{
return false;
}
for (int col = 0; col < _simplex.GetLength(1); col++)
{
if (col != pivot.X)
{
_simplex[pivot.Y, col] =
Math.Round(_simplex[pivot.Y, col] /
_simplex[pivot.Y, pivot.X], cprecision);
}
}
_simplex[pivot.Y, pivot.X] = 1;
for (int row = 0; row < _simplex.GetLength(0); row++)
{
if (row != pivot.Y)
{
for (int col = 0; col < _simplex.GetLength(1); col++)
{
if (col != pivot.X)
{
_simplex[row, col] =
Math.Round(_simplex[row, col] -
(_simplex[pivot.Y, col] *
_simplex[row, pivot.X]), cprecision);
}
}
_simplex[row, pivot.X] = 0;
}
}
int tmp = _base[pivot.Y];
_base[pivot.Y] = pivot.X;
for (int ix = 0; ix < _ccolumns.Length; ix++)
{
if (_ccolumns[ix] == pivot.X)
{
_ccolumns[ix] = tmp;
break;
}
}

for (int col = 0; col < _simplex.GetLength(1) - 1; col++)
{
if (_simplex[_simplex.GetLength(0) - 1, col] > 0)
{
return true;
}
}
return false;
}

En cada paso se selecciona una columna y una fila de la matriz _simplex, cuyo elemento se utilizará como pivote para realizar un cambio de base. La posición de este elemento se calcula con la función SelectPivot, que devuelve una estructura Point, con la columna en X y la fila en Y.

A continuación, se dividen todos los valores de esa fila por el elemento pivote y, a los del resto de filas, se les resta el producto del elemento en la fila del pivote por el de la columna del mismo correspondiente a su fila. Los elementos de la columna del pivote quedan todos a 0, excepto el pivote, que queda a 1.

La posición del vector de la base, en el array _base, correspondiente a la fila seleccionada, se intercambia con la posición correspondiente a la columna en el array _ccolumns.

Por último, se comprueba si todos los valores de la última fila valen 0 o son negativos, en cuyo caso se han terminado los cálculos y se devuelve false.

La función SelectPivot selecciona la fila y la columna del elemento que se usará como pivote:

private Point SelectPivot()
{
Point cmm = new Point(-1,-1);
double mmval = double.MinValue;
for (int col = 0; col < _ccolumns.Length; col++)
{
if (_simplex[_simplex.GetLength(0) - 1, _ccolumns[col]] > 0)
{
int row;
double tn =
Math.Round(ThetaN(_ccolumns[col], out row) *
_simplex[_simplex.GetLength(0) - 1,
_ccolumns[col]], cprecision);
if (tn > mmval)
{
mmval = tn;
cmm = new Point(_ccolumns[col], row);
}
}
}
return cmm;
}

Esta función procesa todas las columnas contenidas en el array _ccolumns y selecciona aquella que hace máximo el producto del valor devuelto por la función Thetan, que también devuelve la fila con el elemento candidato a hacer de pivote para esa columna, por elemento de la última fila correspondiente a la columna.

Por último, la función Thetan selecciona, para una determinada columna, la fila donde el cociente del valor de la última columna en esa fila y el valor correspondiente en la columna, es mínimo:

private double ThetaN(int col, out int row)
{
row = -1;
double min = double.MaxValue;
for (int r = 0; r < _simplex.GetLength(0) - 1; r++)
{
if (_simplex[r, col] > 0)
{
double m =
Math.Round(_simplex[r, _simplex.GetLength(1) - 1] /
_simplex[r, col], cprecision);
if (m < min)
{
min = m;
row = r;
}
}
}
return min;
}

La función devuelve dicho cociente mínimo y la fila donde se ha encontrado, que será la fila correspondiente al elemento utilizado como pivote.