Maximize or minimize a function with the Simplex method
There is a very common problem in linear programming which consists to find the values that make maximum or minimum the value of a linear function, given a number of restrictions on the values of their variables. For example, you may want to find a minimum cost or maximum production function. To do this, there is an algorithm developed in 1947 by George Dantzig, called Simplex, which allows perform such calculations in a simple and effective way.
The function for which we want to find the maximum or minimum value is called target function, and should be a linear function of n variables, in the form:
A1x1 + A2x2 + … + Anxn
Being An any positive or negative number.
The constraints are any number of conditions, in the form of inequations, which must accomplish the variables so that the solution is valid. If the target is to maximize the function, they must be written as follows:
B1x1 + B2x2 + … + Bnxn <= C
Whereas if you want to minimize it, they must be written in the form:
B1x1 + B2x2 + … + Bnxn >= C
Where B and C can be any number, positive, negative or 0.
In this link you can find a mathematical approach to the Simplex method, and in this other you can download the Simplex project, with the sample code accompanying this article, written in csharp with Visual Studio 2013.
The use of the application is very easy; just enter the equation and its restrictions, one per line:
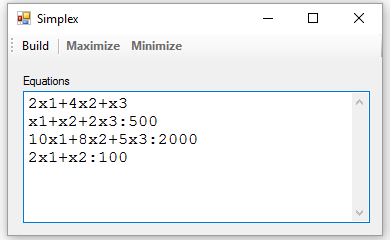
In the first line you have to write the target function, and the constraints, in an unlimited number, in the following lines, without leaving any blank lines. As the inequation changes depending if the operation is for maximize or minimize, I have replaced the symbols <= and >= by the sign : that will be interpreted as one of the above, as appropriate.
The variables can have any name that starts with a letter, followed by any number of alphanumeric characters, numbers can have decimal places, and you can use the + or - sign to link the terms of the equations. If you are interested in this topic, in this link you can find a series of articles on the design of the grammar for an expressions analyser, along with a sample implementation
Once the equations are written, you have to press the Build button to compile them, and then, you can press the Maximize or Minimize button and the program will calculate the values of the variables that make the function maximum or minimum with the given constraints.
In the program, the class that is responsible for performing the calculations is SimplexCalculator, and the classes that implement the expression parser will be found in the Expressions folder. Of these, the most important ones are Expression, which implements the target function, and its derived class, ExConstraint, which implements the constraints. Those classes have a Variables property which provides a list of Variable class objects with all the variables of the expression.
The algorithm consists in construct a matrix with the coefficients of the target function and the constraints, in addition to the canonical basis vectors of a space whose dimension depends on the number of constraints. If, for example, the equation system is as follows:
2x1 + 4x2 + x3
x1 + x2 + 2x3:500
10x1 + 8x2 + 5x3:2000
2x1 + x2 :100
To maximize it, the matrix is constructed as follows:
1 1 2 1 0 0 500
10 8 5 0 1 0 2000
2 1 0 0 0 1 100
2 4 1 0 0 0 0
In the first three columns are the coefficients of the constraints, in the first rows, and, in the latter, those of the target function. In the following three columns are the canonical base vectors, in this case of three dimensions, since there are three constraints. In the last column are the constants that limit the values of the variables, and, in the last row, the final value of the function, which starts with the value 0.
The algorithm is defined to maximize function, so, if you want to minimize it, you have to rewrite it so that it becomes a maximization problem, transforming the target function Z = AX, with the BX >= C constraints, in the Z = CY function, with the constraints BY <= A.
In the case of the previous system, the matrix for minimizing must be written in the form:
1 10 2 1 0 0 2
1 8 1 0 1 0 4
2 5 0 0 0 1 1
500 2000 100 0 0 0 0
And you will proceed with the same algorithm as for maximizing.
In the case of SimplexCalculator class, the constructor receives as parameters the target function in the target parameter, the list of constraints in the constraints parameter, and the maximize parameter, which is true when you want to maximize the function, and false to minimize it.
The constructor calls the CreateArray function, which is responsible for building the matrix with the initial data from the expressions.
The working array is a two-dimensional one, of type double, the first dimension for the rows and the second for the columns, which is stored in the _simplex variable. The coefficients of the expressions are obtained with the method Coefficient of the Expression class, passing it the variable whose coefficient you want to extract as a parameter.
It also build an array in the _base variable that will contain the indices of the columns with the vectors of the base, which will be moving from its place as they are performed the calculations. In another array, in the _ccolumns variable, they are stored the indices of the columns we use to perform calculations, which will also be moving from its place on each step of the algorithm, when the basis change is performed.
The list of variables of the target function are stored in a list in the _lvars variable.
Once the object is built, to perform calculations simply call the Calculate function, that will return the maximum or minimum value and assigns the final value to the different variables of the target function.
public double Calculate()
{
while (PerformStep()) ;
if (_maximize)
{
for (int ib = 0; ib < _base.Length; ib++)
{
if (_base[ib] < _lvar.Count)
{
_lvar[_base[ib]].Value =
_simplex[ib, _simplex.GetLength(1) - 1];
}
}
}
else
{
for (int iv = 0; iv < _lvar.Count; iv++)
{
_lvar[iv].Value =
-_simplex[_simplex.GetLength(0) - 1, iv + _ccolumns.Length];
}
}
return -Math.Round(_simplex[_simplex.GetLength(0) - 1,
_simplex.GetLength(1) - 1], cprecision);
}
This function repeatedly calls another function, PerformStep, which performs each of the steps of the algorithm until the entire process is complete and it returns false. Then, the final values are assigned to the different variables. In the case of a maximization, they will be obtained from the last column of the _simplex array, the positions stored in the _base array will contain the indices of the variables to which must be assigned each.
For the minimization, the values of the variables will be in the last row of the _simplex array, at the initial positions of the basis vectors.
The maximum or minimum value of the function is obtained from the position corresponding to the last row and last column of the _simplex array.
The PerformStep function performs each of the steps of the algorithm:
private bool PerformStep()
{
Point pivot = SelectPivot();
if ((pivot.X < 0) && (pivot.Y < 0))
{
return false;
}
for (int col = 0; col < _simplex.GetLength(1); col++)
{
if (col != pivot.X)
{
_simplex[pivot.Y, col] =
Math.Round(_simplex[pivot.Y, col] /
_simplex[pivot.Y, pivot.X], cprecision);
}
}
_simplex[pivot.Y, pivot.X] = 1;
for (int row = 0; row < _simplex.GetLength(0); row++)
{
if (row != pivot.Y)
{
for (int col = 0; col < _simplex.GetLength(1); col++)
{
if (col != pivot.X)
{
_simplex[row, col] =
Math.Round(_simplex[row, col] -
(_simplex[pivot.Y, col] *
_simplex[row, pivot.X]), cprecision);
}
}
_simplex[row, pivot.X] = 0;
}
}
int tmp = _base[pivot.Y];
_base[pivot.Y] = pivot.X;
for (int ix = 0; ix < _ccolumns.Length; ix++)
{
if (_ccolumns[ix] == pivot.X)
{
_ccolumns[ix] = tmp;
break;
}
}
for (int col = 0; col < _simplex.GetLength(1) - 1; col++)
{
if (_simplex[_simplex.GetLength(0) - 1, col] > 0)
{
return true;
}
}
return false;
}
At each step, a column and a row of the _simplex matrix is selected, which element will be used as a pivot for a basis change. The position of this element is calculated using the SelectPivot function, which returns a Point structure with the column in X and the row in Y.
Then all values in that row are divided by the pivot element, and, for each of the elements on the rest of rows, we subtracts them the product of the element in the pivot row by this in the same column corresponding to their row. The elements in the pivot column are set to 0, except the pivot itself, which is set to 1.
The position of the base vector, in the _base array, corresponding to the selected row, is exchanged with the corresponding column position in the _ccolumns array.
Finally, it is checked whether all the values in the last row are all 0 or negative, in which case the calculations have been completed and the function returns false.
The SelectPivot function selects the row and column of the item to be used as a pivot:
private Point SelectPivot()
{
Point cmm = new Point(-1,-1);
double mmval = double.MinValue;
for (int col = 0; col < _ccolumns.Length; col++)
{
if (_simplex[_simplex.GetLength(0) - 1, _ccolumns[col]] > 0)
{
int row;
double tn =
Math.Round(ThetaN(_ccolumns[col], out row) *
_simplex[_simplex.GetLength(0) - 1,
_ccolumns[col]], cprecision);
if (tn > mmval)
{
mmval = tn;
cmm = new Point(_ccolumns[col], row);
}
}
}
return cmm;
}
This function processes all the columns contained in the _ccolumns array and select the one that maximizes the product of the value returned by the Thetan function, which also returns the row with the element candidate to pivot for that column, by the element of the last row corresponding to that column.
Finally, the Thetan function selects, for a given column, the row where the quotient of the value of the last column in that row and the corresponding value in the column, is minimal:
private double ThetaN(int col, out int row)
{
row = -1;
double min = double.MaxValue;
for (int r = 0; r < _simplex.GetLength(0) - 1; r++)
{
if (_simplex[r, col] > 0)
{
double m =
Math.Round(_simplex[r, _simplex.GetLength(1) - 1] /
_simplex[r, col], cprecision);
if (m < min)
{
min = m;
row = r;
}
}
}
return min;
}
The function returns this minimum quotient and the row where it has been found, that will be the row corresponding to the element used as a pivot.









