How to build an expressions analyzer, the implementation (II)
In the previous article in this series I began to show how to implement an arithmetic expression analyzer, or parser, from the grammar rules in BNF notation, with classes which extract numbers, variables and constants. In this article I will finish the series with the implementation of the class focused in working with the main rule, which analyzes the expressions themselves. I will also provide a small sample application that draws the graph corresponding to the expression from the object generated by the compiler.
If you prefer to start at the beginning, this is the link to the article on the design of the grammar for an expressions analyser.
In this link you can download the source code of the project with the parser I will use as an expample in this article, written in CSharp with Visual Studio 2013.
The Expression class
The Expression class is those with the highest level in the parser. The compiler will generate as a result an object of this type, whose variables and constants may be obtained to give its values using the Variables and Constants properties, and that can be evaluated by reading their Value property. These are the BNF rules from which I have built the class:
<expr>::=<expr2>+<expr>|<expr2>-<expr>|<expr2>
<expr2>::=<expr1>*<expr2>|<expr1>/<expr2>|<expr1>
<expr1>::=<expr0>^<expr1>|<expr0>
<expr0>::=-<element>|<element>
<element>::=(<expr>)|<number>|<const>|<var>
The class represents the rule <expr>. The remaining rules, <element>, <expr0>, <expr1> and <expr2>, are implemented as functions within the class. Recall that I have derived the rules involving different operators according to their level of precedence.
The expression operands are stored in the _operand1 and _operand2 variables, and the operator in the _operator variable. The Value property performs the corresponding operation between the two operands:
public override double Value
{
get
{
if (_operand2 == null)
{
if (_operator == '-')
{
return -_operand1.Value;
}
return _operand1.Value;
}
switch (_operator)
{
case '+':
return Math.Round(_operand1.Value + _operand2.Value,
ExpressionBase._precision);
case '-':
return Math.Round(_operand1.Value - _operand2.Value,
ExpressionBase._precision);
case '*':
return Math.Round(_operand1.Value * _operand2.Value,
ExpressionBase._precision);
case '/':
return Math.Round(_operand1.Value / _operand2.Value,
ExpressionBase._precision);
case '^':
return Math.Round(Math.Pow(_operand1.Value, _operand2.Value),
ExpressionBase._precision);
default:
return double.NaN;
}
}
set
{
throw new NotSupportedException();
}
}
The Parse method begins with the analysis of the input string and processes the sum and difference operations:
public override string Parse(string expr)
{
string sexpr = base.Parse(expr);
if (!string.IsNullOrEmpty(sexpr))
{
_operand1 = Expression2(ref sexpr);
sexpr = base.Parse(sexpr);
while (!string.IsNullOrEmpty(sexpr))
{
if (sexpr[0] == ')')
{
return sexpr;
}
else if ((sexpr[0] == '+') || (sexpr[0] == '-'))
{
if (_operand2 != null)
{
_operand1 = new Expression(_operand1, _operand2,
_operator);
}
_operator = sexpr[0];
if (sexpr.Length > 1)
{
sexpr = base.Parse(sexpr.Substring(1));
_operand2 = Expression2(ref sexpr);
sexpr = base.Parse(sexpr);
}
else
{
throw new BadSyntaxException(sexpr);
}
}
else
{
throw new BadSyntaxException(sexpr);
}
}
if ((_operand2 == null) && (_operator != '-'))
{
Expression exp = _operand1 as Expression;
if (exp != null)
{
_operand1 = exp._operand1;
_operand2 = exp._operand2;
_operator = exp._operator;
}
}
return sexpr;
}
throw new NotRecognizedException();
}
In this method we can detect the end of a parenthetical expression in order to avoid a syntax error. This method can return both a new expression as a single element, such as a number, variable or constant, so that the expression is optimized in the cases where the remainder is one of these elements instead of a new expression.
With the Expression2 method an expression whose operation is a product or a division is generated:
private ExpressionBase Expression2(ref string expr)
{
ExpressionBase operand1 = Expression1(ref expr);
ExpressionBase operand2 = null;
char op = '\0';
expr = base.Parse(expr);
while (!string.IsNullOrEmpty(expr))
{
if ((expr[0] == '*') || (expr[0] == '/'))
{
if (operand2 != null)
{
operand1 = new Expression(operand1, operand2, op);
}
op = expr[0];
if (expr.Length > 1)
{
expr = base.Parse(expr.Substring(1));
operand2 = Expression2(ref expr);
expr = base.Parse(expr);
}
else
{
throw new BadSyntaxException(expr);
}
}
else
{
break;
}
}
if (operand2 != null)
{
return new Expression(operand1, operand2, op);
}
return operand1;
}
The same thing for the exponentiation, in the Expression1 method, and unary minus, in the Expression0 method. In the lowest level method, Element, we start trying to build a number:
try
{
Number exnum = new Number();
expr = exnum.Parse(expr);
return exnum;
}
catch (NotRecognizedException ex) {}
We must catch the NotRecognizedException exception, so that a false syntax error does not occur. We must also check the same way if the next element is a variable or a constant:
try
{
Variable exvar = new Variable();
expr = exvar.Parse(expr);
return ExpressionBase._variables[ExpressionBase._variables.IndexOf(exvar)];
}
catch (NotRecognizedException ex) {}
try
{
Constant excon = new Constant();
expr = excon.Parse(expr);
return ExpressionBase._constants[ExpressionBase._constants.IndexOf(excon)];
}
catch (NotRecognizedException ex) {}
And, finally, we check if it is a new expression between parentheses:
if (expr[0] == '(')
{
if (expr.Length > 1)
{
expr = base.Parse(expr.Substring(1));
ExpressionBase expar = new Expression();
expr = expar.Parse(expr);
expr = base.Parse(expr);
if (!string.IsNullOrEmpty(expr))
{
if (expr[0] == ')')
{
if (expr.Length > 1)
{
expr = expr.Substring(1);
}
else
{
expr = "";
}
return expar;
}
}
}
}
And with this we have the parser completed and we can generate executable objects with the Expression class. Then I will show how to use these objects with a simple application that draws the graph corresponding to the expression and allows change the values of their constants and variables.
The ExpressionPlayer application
This sample application is limited to compile an expression and represent their graph in two dimensions, with the main variable on the x-axis and one or two TrackBar controls to modify the value of the other variables, if they exist:
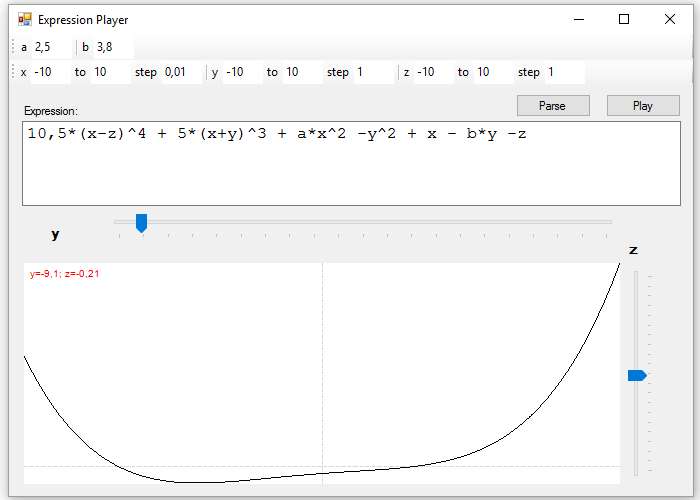
Once written expression, just press the Parse button to try to compile it. If the syntax is correct, you get an object of the Expression type
Expression _expr = new Expression();
_expr.Parse(txtExpression.Text);
The program will create controls on the toolbar that allow us to assign values to the constants and set a range of values for the variables, and provide the step between two successive values of the variable. Once these values are set, just press the Play button to draw the graph. You can change the value of the secondary variables using the TrackBar to verify how to the shape of the graph is modified.
And this is all about implementing a parser to work with arithmetic expressions. The code can be extended to work with more sophisticated expressions without further to add new rules to the grammar and implement them in the appropriate classes.
As in previous articles, I leave a list of books that can help you go deeper into the topic:









