Logical calculation with Tableaux
The Tableaux is a logical calculus tool that is very useful to demonstrate a conclusion from a set of premises, find counterexamples or models of a set of logical formulas or demonstrate that a formula is a tautology, i.e., that is true in all possible cases. They can be used in artificial intelligence as the basis for implementing automated theorem proving.
Although the Tableaux can be used with multiple logical systems, in this article, for simplicity, I will only apply it to predicate logic.
In this link you can download the Tableaux project whit an example of implementation, written in CSharp with Visual Studio 2013.
The program looks like this:
In the Premises and Conclusion text editors you can write formulas of predicate logic using the following connectives: ! for negation, & for conjunction (logical AND), | for disjunction (logical OR) -> for the implication and <-> for the double implication, although the latter two will be converted internally in formulas composed exclusively of negations, conjunctions and disjunctions:
A -> B becomes !A | B, and A <-> B becomes (!A | B) & (!B | A).
The classes used to compile and manage the formulas are in the Formulas folder of the Tableaux project, and are based on the design of the parser of the article design of the grammar for an expressions analyser.
The operator with the highest precedence is the negation, followed by implication and double implication, and finally, the conjunction and disjunction. You can use parentheses to change the precedence rules.
The procedure used by the Tableaux is very simple. It starts of the set of premises, which are written each one on a line in the Premises text editor, and the conclusion negated, since the Tableaux attempts to refute that the conclusion follows from the premises (or that the conclusion is not a contradiction, if there is no premises).
These formulas are the initial branch of the Tableaux. From here you can perform two type of operations, with conjunctive formulas (which can be written as two sub formulae linked together by the & connective) or disjunctive ones (ditto, with the | connective).
At each step, an appropriate formula from anywhere in the Tableaux is selected. Conjunctive formulas are divided into those two at the sides of the connective, and they are added at the end of the current branch. This operation can only be done if in the branch does not already appear none of the sub formulae, looking from the tree root to the end of this sub-branch.
With the disjunctive formulas, the current branch is divided in two sub-branches, each one starting with one of the sub formulae at the two sides of the connective. The same rule as in the previous case is applied: none of the sub formulae can be already present in the sub-branch.
When a formula and its negation appears in a branch, this branch is considered closed and it can no longer be used to expand the Tableaux.
This process is repeated until no more operations can be performed. At this time, the Tableaux is finished. If all its branches are closed, it is considered proven the conclusion from the premises, otherwise, the conclusion does not follow from the premises, and we can get counterexamples from the branches that are open. The propositions that are not part of a formula and appear negated in those branches are considered to be having a FALSE value; those that don’t are negated have a TRUE value.
If you want to prove that a formula is a tautology, simply left blank the Premises text editor and write only the conclusion. If you only write a set of premises, but do not provide any conclusion, the Tableaux check whether the set of premises is satisfiable (that is, certain truth values can be assigned to the propositions to make true all the premises) and, if that is the case, shows those sets of values, which are the models of the set of formulas.
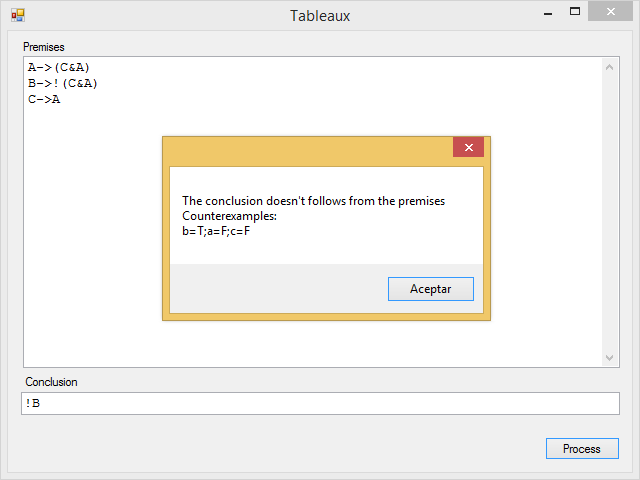
The program will also show a schema of the steps followed to solve the Tableaux. For example, given the following set of premises:
A -> (C & A)
B -> !(C & A)
C -> A
And the conclusion:
!B
The application displays the following message with a counterexample (since the conclusion does not follow from the premises):
And it will show the Tableaux schema that has been built to achieve this result:
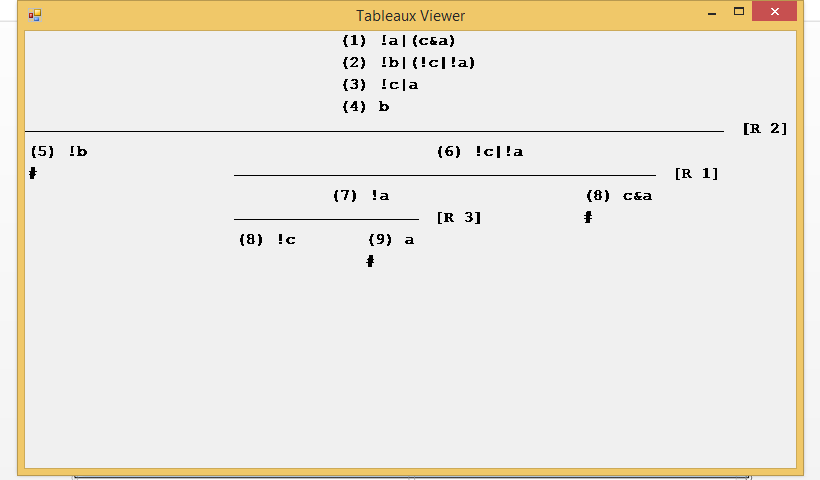
Each one of the formulas is numbered on the right side, and, enclosed in brackets, which of them has been used to apply the rule to extend or divide the branches. The closed branches end with a # character.
There is not a single way to build the Tableaux, because normally there are several formulas that are valid candidates for applying the rules, but the final conclusion is always the same. In the case of this implementation, it has applied the following heuristics to select candidate formulas: a conjunctive formula is preferably selected to avoid making too many branches, and it always tries to select a formula that closes a branch when the rule is applied.
Brief explanation of the source code of the Tableaux program
To not extend too much this article, this time I'll make only a brief explanation of the main classes in the source code of the Tableaux project.
There are two classes that implement the elements of the Tableaux, TableauxElementAlpha, which manages the branches that are formed by adding formulas when the rule for conjunctive formulas is applied, and TableauxElementBeta, which manages the ramifications that are formed by applying the rule to the disjunctive formulas. Both inherit from the abstract base class TableauxElementBase.
The TableauxElementAlpha class stores the formulas in a list of KeyValuePair objects, whose key is the index of the formula that has been applied to extract the sub formula, or -1 if it is one of the formulas in the initial set. The _branch variable also contains a KeyValuePair object, which contains a TableauxElementBeta object, along with the index of the formula from which it has been constructed, when the branch is divided into two sub branches.
The TableauxElementBeta class contains two TableauxElementAlpha sub branches, stored in the _fleft and _fright variables.
The properties and common methods are defined in the abstract base class TableauxElementBase, and are as follows:
- Closed: This property indicates whether the sub-branch is closed.
- Models: It is a method that returns a list of text strings with the values of the variables that constitute a counterexample or a model of the set of input premises.
- Contains: This function checks in the sub-branch if exists the formula that is passed as a parameter. It can be used to check whether a particular rule can be applied on the sub-branch, or to check whether the sub-branch is closed or will close, passing the negated formula in the parameter.
- PerformStep: This is the highest level method; that is called to execute the next step in the Tableaux. It will return true if it was possible to perform a step, or false otherwise.
- WhatIf: With this method we check what would happen in the Tableaux in the case of applying a certain rule in the current branch. It returns a member of the StepResult enumeration, that can be NotAllowed, to indicate that it is not possible to perform the operation, BranchClosed, to indicate that the branch will close, or None, to indicate that nothing relevant will happen.
The CalcRect and Draw methods are simply used to draw the schema of the Tableaux calculated.
The class that manages the Tableaux is TableauxCalculator, through its Calculate method.









