Extensión II de WinRQA, series de medidas de recurrencia
WInRQA es una aplicación dedicada a los mapas de recurrencia, una herramienta que se utiliza en el análisis de recurrencia de series temporales complejas. En este artículo voy a presentar una nueva herramienta que he añadido al programa. Hasta ahora, las medidas de cuantificación de recurrencia (RQM) se obtenían solamente a partir de una porción estática de la serie original. Con la nueva herramienta, podremos obtener una serie de medidas desplazando una ventana a lo largo de toda la serie original y calculando las medidas correspondientes a cada una de dichas ventanas.
Para los detalles técnicos sobre este tipo de análisis, te puedo recomendar este sitio web dedicado por entero a los mapas de recurrencia, o este libro que trata sobre los mapas de recurrencia y su análisis.
En este enlace puedes descargar el ejecutable del programa WinRQA, y, en este otro, puedes descargar el código fuente del proyecto WinRQA, escrito en CSharp con Visual Studio 2013. Se trata de una aplicación para Windows, versión 7 o posterior.
En este otro enlace puedes encontrar el primer artículo de la serie sobre la aplicación WinRQA.
Generar series para obtener medidas de recurrencia
Para que podáis ver en que consiste la nueva herramienta, vamos a generar en primer lugar alguna serie de ejemplo, para ello voy a utilizar el programa R. Si os queréis ahorrar esta parte, en este enlace podéis descargar los ficheros csv con las series generadas.
Vamos a utilizar la función logística para generar las series. Se trata de una ecuación muy simple, con un solo parámetro y que se define de forma recursiva:
Xn+1 = uXn(1-Xn)
El parámetro u puede variar entre 1 y 4, mientras que X se mantiene siempre en el intervalo (0,1). Esta serie presenta diferentes tipos de dinámica en función del valor del parámetro u, para valores inferiores a 3,57, aproximadamente, la serie presenta una dinámica estacionaria o periódica, pero, a partir de este valor, la dinámica se vuelve caótica, aumentando el grado de caoticidad a medida que nos acercamos a 4, aunque con una pequeña zona periódica alrededor de 3,83.
Este es un diagrama de Feigenbaum en el que podéis ver como varía el número de términos diferentes de la serie en función del valor del parámetro u:
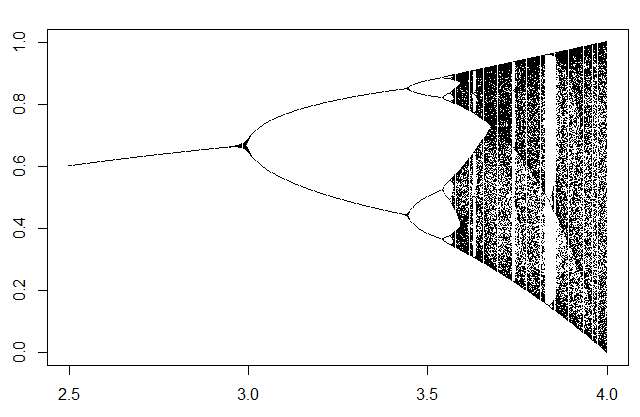
Esto nos va a permitir generar una serie con diferentes dinámicas. En primer lugar, definiremos un par de funciones auxiliares, podéis editar un script con ellas y guardarlo en el directorio de trabajo. Yo le he puesto el nombre dlogistic.R:
dfLog<-function(length, initial) {
u<-3;
du<-1/length;
c<-1:(length);
c[1] <- initial;
for (i in 2:(length)) {
v<-u*c[i-1]*(1-c[i-1]);
c[i]<-v;
u<-u+du;
}
return(c);
}
fLog<-function(u,length,initial) {
c<-1:length;
c[1]<-initial;
for (i in 2:length) {
c[i]<-u*c[i-1]*(1-c[i-1]);
}
return(c);
}
La función dfLog genera una serie de length valores, con el valor inicial initial. El parámetro u va variando a lo largo de la serie desde un valor de 3 a un valor final de 4, con lo que la serie pasa por diferentes tipos de dinámica. Esta es una serie de 2000 valores, por ejemplo:
source("dlogistic.r")
c<-dfLog(2000,0.5)
plot(c,type="l")
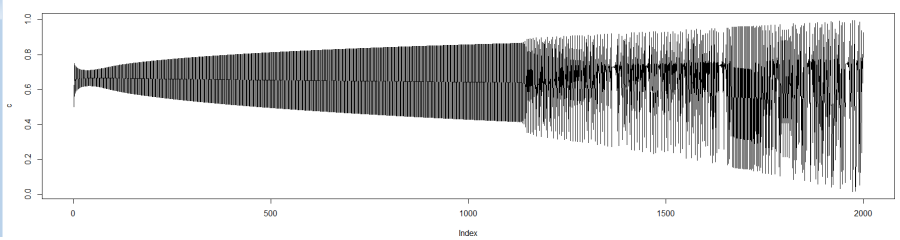
A continuación, lo grabamos en el archivo dlog.csv:
write.csv(c,"dlog.csv",row.names=F)
Antes de poder cargarlo en la aplicación, habrá que quitarle la primera fila, con el nombre de la columna.
Podemos generar otro fichero con una serie con solo dos dinámicas diferentes, usando la función fLog, a esta función le pasamos el parámetro u con el que queremos generar la serie:
c<-fLog(3.78,1000,0.5)
c<-c(c,fLog(3.98,1000,c[1000]))
plot(c,type="l")
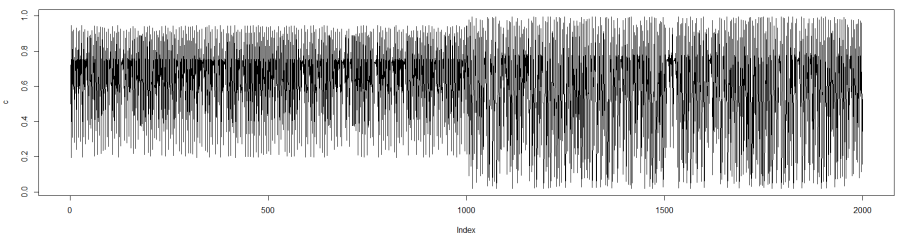
Que también podemos guardar en un archivo (no olvides eliminar la primera fila):
write.csv(c,"logistic2.csv",row.names=F)
Estudio de una serie temporal mediante series de medidas de recurrencia
Con estas dos series generadas, podemos probar la nueva herramienta que he añadido al programa WinRQA. Vamos a abrir el archivo dlog.csv. En la barra de herramientas se encuentra aparece el botón SMCR con el que podemos lanzarla. Pero antes, habrá que ajustar el parámetro Radio a un valor mayor o igual que cero (un buen valor para esta serie es 0,1), pues con valores menores que cero no se generan medidas de recurrencia.

Una vez que lanzamos la herramienta, aparece un formulario con una barra de herramientas como esta:

La serie tiene 2000 valores. En los cuadros de texto de la barra de herramientas superior podemos definir el punto inicial y final de la serie que vamos a procesar, el paso entre punto y punto y el tamaño de la ventana que vamos a utilizar para construir cada mapa de recurrencia.
En la barra de herramientas inferior, podemos ver todas las medidas de recurrencia, con un recuadro blanco a la derecha, y un botón marcado con una paleta de colores que nos permite seleccionar un color para la gráfica de esa medada. Solo se dibujarán las gráficas de las medidas que tengan un color diferente del blanco. Al seleccionar las medidas que vamos a añadir a la gráfica, hay que tener en cuenta que los rangos de valores pueden variar bastante entre unas y otras, por lo que algunas gráficas pueden aparecer como una línea recta por efecto únicamente de la escala.
Una vez seleccionadas las medidas, podemos lanzar el cálculo con el primer botón de la barra de herramientas superior. Aparecerá una gráfica como esta:

Aunque la serie pasa de una dinámica periódica a una caótica más o menos a partir de la posición 1100, con esta herramienta podemos detectar el cambio de dinámica con bastante antelación, a partir de la posición 950, aproximadamente.
Aunque la dinámica periódica al principio de la serie es variable, podemos ver que las medidas en esa zona siguen una línea recta. El mapa de recurrencia capta el tipo de dinámica, más que otras características de la señal, como su intensidad o periodo.
Algunas de las medidas son más apropiadas que otras para detectar cambios sustanciales en la serie y su dinámica, o para caracterizar determinados estados respecto de otros. Con esto ya tenemos la base para realizar análisis de recurrencia de series temporales.
También hay que tener en cuenta que esta señal está generada artificialmente, por lo que carece de ruido. En general, las señales procedentes del mundo real tienen una cierta cantidad de ruido que muchas veces enmascara sus características, lo que se refleja en los valores de las medidas de recurrencia. Un buen filtrado de la serie, siempre que sea posible, favorece la exactitud del análisis.
Si queremos guardar en un archivo las series de medidas calculadas por el programa, en el menú Archivo existe la opción Guardar CSV… (Cuando este formulario está seleccionado) con la que podéis guardar un fichero con las medidas calculadas y la posición de la serie a la que pertenece cada una de ellas. Con esto, podemos realizar un análisis en profundidad de los datos con una herramienta como el programa R.
Este archivo csv tiene nombres de columnas en la primera fila, la primera columna contiene la posición en la serie y los datos se separan utilizando el carácter punto y coma (;). Los lugares decimales de los números se separan con el carácter punto (.).
Podéis probar con la otra serie, logistic2.csv, que tiene una diferencia menor entre las dos zonas con diferente dinámica. Tened en cuenta que la dinámica cambia a partir de la posición 1000, pasando de caótica a más caótica todavía.









