Tableaux para lógica de primer orden

El Tableaux es una herramienta de cálculo lógico que permite comprobar la validez de una conclusión a partir de una serie de premisas. En el artículo anterior he explicado brevemente los fundamentos del cálculo con Tableaux para lógica de predicados, en este artículo voy a extender el programa a la lógica de primer orden, que tiene mucha más capacidad expresiva que la lógica de predicados, aunque esto también hace mucho más difícil el cálculo automático.

En este enlace puedes descargar el proyecto FOTableaux, con el código fuente y el ejecutable del programa, escrito en CSharp con Visual Studio 2013.

Empecemos con una revisión de los elementos de la lógica de primer orden. En primer lugar, tenemos los términos:

• Constantes, que representan un individuo concreto, y que en el programa se deben escribir siempre empezando por el carácter ‘_’, seguido de una letra y cualquier número de caracteres alfanuméricos. También se pueden usar como constantes los números naturales.
• Variables, que representan un individuo genérico. En el programa se diferencian de las constantes porque su nombre no comienza por el carácter ‘_’, sino por una letra cualquiera, seguida de cualquier número de caracteres alfanuméricos.
• Funciones, que son términos compuestos, pues tienen parámetros que deben ser también términos. En el programa las funciones se escriben con un nombre que empieza con cualquier letra seguida de cualquier número de caracteres alfanuméricos y una lista de parámetros separados por comas encerrados entre paréntesis, por ejemplo: f(x,y,_c). El resultado de una función es un individuo, es decir, un término. Por ejemplo “el padre de x” es una función.

Las fórmulas se construyen utilizando los siguientes elementos:

• Los símbolos Verdadero y Falso, son fórmulas.
• Una proposición o relación, referida a 0 o más términos, es una fórmula. Se escriben con una letra seguida de cualquier número de caracteres alfanuméricos, con la lista de términos a los que hace referencia separados por comas y encerrados entre corchetes. Los corchetes se deben poner aunque la proposición no tenga parámetros. Por ejemplo “x e y son amigos” es una relación, y se escribiría AM[x,y].
• Una igualdad es una fórmula. Consiste en dos términos conectados con el operador =, por ejemplo x = y.
• Una fórmula a la que se le aplica el operador NOT de negación lógica, es una fórmula.
• Dos fórmulas conectadas por los operadores lógicos AND, OR, implicación y doble implicación es también una fórmula.
• Existen unos elementos, llamados cuantificadores, que se refieren a una determinada variable de una fórmula y que pueden referirse a todos los posibles individuos (cuantificador universal) o solamente a uno o más individuos (cuantificador existencial). Una fórmula a la que se le aplica un cuantificador es también una fórmula.

Aunque el uso del programa en esta versión es básicamente igual que en el artículo anterior, he modificado los símbolos para que las fórmulas aparezcan escritas con un formato más estándar, estas son las teclas y los símbolos a los que dan lugar:

• Operador AND, se obtiene pulsando la tecla &, pero el símbolo que aparece es el caracter ˄.
• Operador OR, se obtiene pulsando la tecla |, pero el símbolo que aparece es el caracter ˅.
• Implicación: pulsando la tecla < se obtiene el caracter →.
• Doble implicación: pulsando la tecla > se obtiene el caracter ↔.
• Cuantificador universal: se obtiene pulsando la tecla @.
• Cuantificador existencial: se obtiene pulsando la tecla #.
• Verdadero, se obtiene pulsando la tecla $, el símbolo es ⟙.
• Falso, se obtiene pulsando la tecla %, el símbolo es ⟘.

Se pueden utilizar paréntesis para agrupar fórmulas, por ejemplo, no es lo mismo PT[x]→(PQ[x]˅PL[x]˅SV[x]) que PT[x]→PQ[x]˅PL[x]˅SV[x] pues, en este programa, el operador implicación tiene mayor precedencia que el operador OR o AND.

Las igualdades deben escribirse entre paréntesis si se quieren negar. En general, es mejor escribir siempre las igualdades entre paréntesis.

También se utilizan paréntesis para aplicar un cuantificador a toda una fórmula compuesta, como por ejemplo ᗄx(PT[x]→(PQ[x]˅PL[x]˅SV[x])). Si no ponemos los paréntesis, el cuantificador solo se aplicaría a la primera subfórmula, PT[x].

El programa siempre transforma las implicaciones en sus fórmulas equivalentes usando las conectivas AND y OR y el operador NOT. También resuelve las negaciones de fórmulas compuestas antes de procesar el Tableaux.

Este es el aspecto del programa:

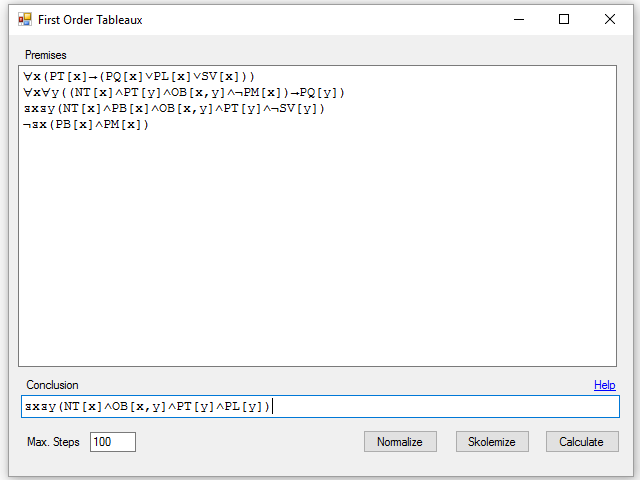
A la funcionalidad del Tableaux para lógica de predicados le he añadido los siguientes elementos:

• Número máximo de pasos (Max Steps). Un Tableaux de primer orden puede ser infinito, además, es posible que con un conjunto muy complejo de fórmulas el programa no sea capaz de encontrar el desarrollo apropiado para terminar el Tableaux. Para evitar que el programa se quede colgado, se puede indicar el número máximo de fórmulas a desarrollar antes de que el programa de por imposible la resolución.
• Normalización. Con este botón, todas las fórmulas se reescriben en forma prenexa, que consiste en pasar al principio de la fórmula todos los cuantificadores. No es necesario usar esta opción para calcular el Tableaux, pero puede servir para corregir ejercicios, por ejemplo.
• Skolemizacion: Consiste en pasar las fórmulas a forma normal de Skolem, una forma prenexa en la que los cuantificadores existenciales se han eliminado y sus variables cuantificadas se han sustituido por constantes o funciones apropiadas. Las constantes y funciones introducidas en este paso se nombran usando la siguiente estructura: *sk + numero de orden. Para calcular el Tableaux no es recomendable usar la normalización de Skolem para las fórmulas, ya que la sustitución de variables y funciones se realiza fórmula a fórmula, y puede cambiar el sentido de la argumentación. Esta opción se puede utilizar para corregir ejercicios.

Como resultado obtenemos dos formatos diferentes para visualizar el Tableaux, más o menos apropiados según el tamaño del resultado. Por un lado, se obtiene una vista de árbol desplegable, en la que las ramificaciones se pueden expandir o contraer y contienen la lista de fórmulas hasta el siguiente nodo en el que se ramifica el Tableaux, esta vista es más apropiada para conjuntos grandes de fórmulas.

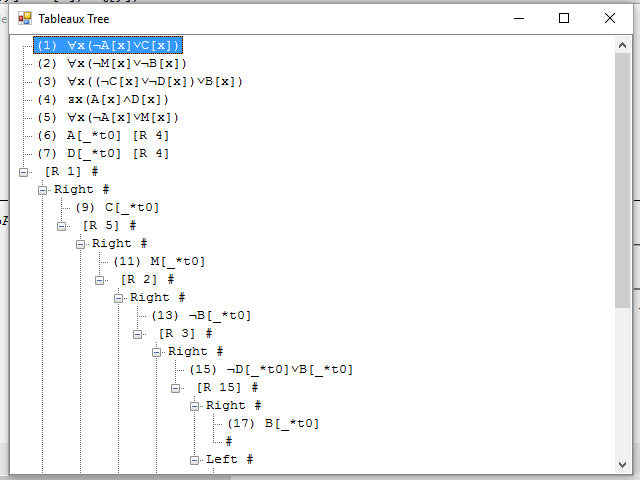
Las ramas cerradas se indica con el símbolo #, como en el Tableaux para lógica de predicados, y el número de la fórmula que se ha utilizado para crear otras nuevas o realizar una ramificación se indica entre corchetes, después de la letra R.

La existencia del operador de igualdad introduce dos nuevas reglas de creación de fórmulas. Por un lado, está la regla de reflexividad, indicada por las letras RF, que permite introducir al final de una rama la fórmula t = t, siendo t un término cualquiera de los que aparecen en la rama. También podemos utilizar la regla de sustitución, indicada por las letras ST, que nos permite sustituir en una fórmula cualquiera de la rama el término t por el término t’, siempre que exista una fórmula de la forma t = t’ en la rama.

Para crear nuevas fórmulas a partir de las fórmulas con cuantificadores, en el caso de los cuantificadores existenciales, sustituiremos la variable cuantificada por una nueva constante, llamada ejemplo, que no se haya utilizado ya en la rama. Solo puede haber un ejemplo de fórmula cuantificada existencialmente en una misma rama. Las variables cuantificadas por cuantificadores universales las podemos sustituir por cualquier término de los utilizados en la rama, o por una nueva constante, en caso de que no exista ningún término disponible. Estas constantes o funciones, introducidas para particularizar fórmulas cuantificadas, se nombran siempre siguiendo el esquema *t + número secuencial.

También obtenemos una vista del Tableaux totalmente desplegada que puede ser útil cuando el número de fórmulas no es demasiado elevado:

Este Tableaux puede usarse también para resolver cualquier problema de lógica de predicados, ya que esta es un subconjunto de la lógica de primer orden. Sin embargo, la heurística empleada para intentar resolver los Tableaux de primer orden no va más allá del siguiente paso, por lo que es posible que haya que mejorar bastante los algoritmos para resolver problemas con conjuntos de fórmulas complejas. El programa resuelve con éxito todos los ejercicios planteados en el libro que utilizo como referencia, y que es el siguiente: Lógica matemática para informáticos