Cálculo lógico con Tableaux

El Tableaux es una herramienta de cálculo lógico que resulta muy útil para demostrar una conclusión a partir de una serie de premisas, encontrar contraejemplos o modelos de un conjunto de fórmulas lógicas o demostrar que una fórmula es una tautología, es decir, que es verdadera en todos los casos posibles. Se pueden utilizar en inteligencia artificial como base para implementar demostradores automáticos de teoremas.

Aunque los Tableaux se pueden utilizar con multitud de sistemas lógicos, en este artículo, por simplicidad, lo voy a aplicar solamente a la lógica de predicados.

En este enlace puedes descargar el proyecto Tableaux que utilizaré como ejemplo de implementación, escrito en CSharp con Visual Studio 2013.

El programa presenta el siguiente aspecto:

En los editores de texto Premises y Conclusion se pueden escribir fórmulas de la lógica de predicados utilizando las siguientes conectivas: ! para la negación, & para la conjunción (AND lógico), | para la disyunción (OR lógico), -> para la implicación y <-> para la doble implicación, aunque estas dos últimas serán convertidas internamente a fórmulas compuestas exclusivamente por negaciones, conjunciones y disyunciones:

A -> B se convierte en !A | B, y A <-> B en (¡A | B) & (¡B | A).

Las clases utilizadas para compilar y gestionar las fórmulas se encuentran en la carpeta Formulas del proyecto Tableaux, y están basadas en el parser del artículo diseño de la gramática para un analizador de expresiones.

El operador con mayor precedencia es la negación, seguido de la Implicación y doble implicación, y, por último, la conjunción y la disyunción. Se pueden utilizar paréntesis para modificar las reglas de precedencia.

El procedimiento que sigue el Tableaux es muy sencillo. Se parte del conjunto de premisas, que se escriben cada una en una línea del editor de texto Premises, y de la conclusión negada, ya que de lo que se trata es de intentar refutar que la conclusión se sigue de las premisas (o que la conclusión no es una contradicción, si no hay premisas).

Estas fórmulas forman la rama inicial del Tableaux. A partir de aquí se pueden realizar dos operaciones con las fórmulas conjuntivas (que se pueden escribir como dos subfórmulas unidas por la conectiva &) o disyuntivas (ídem, con la conectiva |).

En cada paso, se selecciona una fórmula apropiada que aparezca en cualquier parte del Tableaux. Las fórmulas conjuntivas se dividen en las dos subfórmulas a los lados de la conectiva y se añaden al final de la rama actual. Esta operación solamente puede hacerse en el caso de que en la rama no aparezca ninguna de las dos subfórmulas, desde la raíz del árbol hasta el final de dicha subrama.

Con las fórmulas disyuntivas, se divide la rama actual en dos subramas, cada una de las cuáles empieza con una de las subfórmulas a los lados de la conectiva. Se aplica la misma regla que en el caso anterior, ninguna de las subfórmulas debe estar presente ya en la subrama.

Cuando en una subrama aparece una subfórmula y su negación, la rama se considera cerrada y ya no se puede continuar extendiendo.

Este proceso se repite hasta que ya no se pueden realizar más operaciones. En este momento, el Tableaux está terminado. Si todas sus ramas están cerradas, se considera probada la conclusión a partir de las premisas, en caso contrario, la conclusión no se sigue de las premisas, y podemos obtener contraejemplos a partir de las ramas que quedan sin cerrar. Las proposiciones que no forman parte de una fórmula y que aparezcan negadas en dicha rama se considera que deben tener un valor FALSE, mientras que las que no aparezcan negadas deben tener un valor TRUE.

Si queremos probar que una fórmula es una tautología, se dejará en blanco el editor de premisas y se escribirá solamente la conclusión. Si solo escribimos un conjunto de premisas, pero no escribimos ninguna conclusión, el Tableaux comprobará si el conjunto de premisas es satisfacible (se pueden asignar determinados valores de verdad a las proposiciones para hacer verdaderas todas las premisas) y, en caso de que sea así, mostrará dichos conjuntos de valores, que constituyen los modelos del conjunto de fórmulas.

El programa mostrará también un esquema de los pasos seguidos para resolver el Tableaux. Por ejemplo, con el siguiente conjunto de premisas:

A -> (C & A)
B -> !(C & A)
C -> A

Y la conclusión:

!B

El programa presentará el siguiente mensaje con un contraejemplo (ya que la conclusión no se deduce de las premisas):

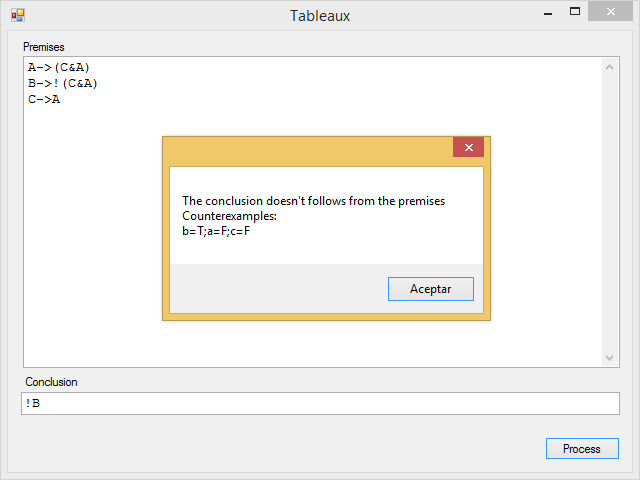
Y mostrará el desarrollo del Tableaux que ha construido para llegar a este resultado:

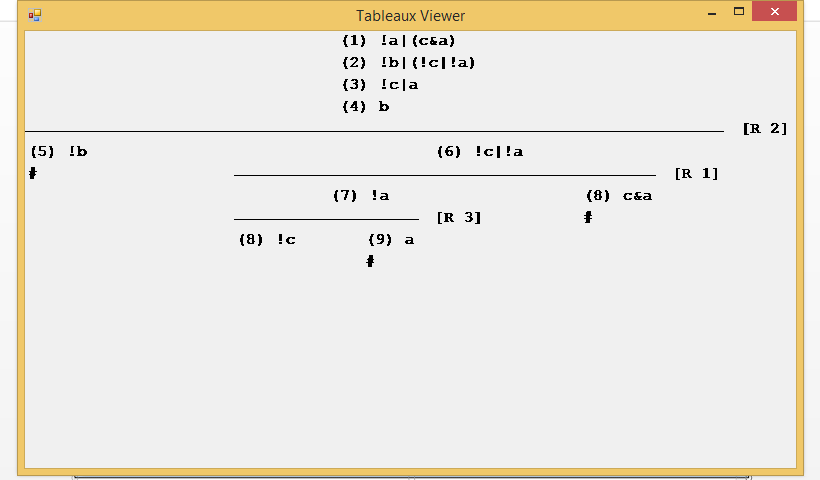
Cada una de las fórmulas está numerada y, a la derecha, se indica entre corchetes cuál de ellas se ha utilizado para aplicar la regla de extensión del conjunto y bifurcación de las ramas. Las ramas cerradas terminan con un símbolo #.

No existe una única forma de construir el Tableaux, ya que normalmente existen varias fórmulas que son candidatas válidas para aplicar las reglas, pero la conclusión final será siempre la misma. En el caso de esta implementación, se ha aplicado la siguiente heurística para seleccionar las fórmulas candidatas: se selecciona preferentemente una fórmula conjuntiva, para evitar hacer demasiadas ramificaciones, y siempre se trata de seleccionar una fórmula que genere una rama cerrada al aplicar la regla.

Breve explicación del código fuente del programa Tableaux

Para no alargar demasiado el artículo, esta vez voy a hacer solo una breve explicación del código fuente del proyecto Tableaux.

Existen dos clases para implementar los elementos del Tableaux, TableauxElementAlpha, que gestiona las ramas que se forman mediante la adición de fórmulas al aplicar la regla para las fórmulas conjuntivas, y TableauxElementBeta, que gestiona las ramificaciones que se forman al aplicar la regla para las fórmulas disyuntivas. Ambas descienden de la clase base abstracta TableauxElementBase.

La clase TableauxElementAlpha almacena las fórmulas en una lista de elementos KeyValuePair, cuya clave es el índice de la fórmula a la que se ha aplicado la regla con la que se ha extraído la subfórmula o -1 si es una de las fórmulas del conjunto inicial. También contiene la variable _branch, que contiene un elemento de la clase TableauxElementBeta, también junto con el índice de la fórmula a partir de la cual se ha formado, para indicar que la rama se divide en dos subramas.

La clase TableauxElementBeta contiene a su vez dos subramas, en forma de objetos TableauxElementAlpha, en las variables _fleft y _fright.

Las propiedades y métodos comunes se encuentran definidos en la clase base abstracta TableauxElementBase, y son las siguientes:

• Closed: esta propiedad indica si la subrama está cerrada.
• Models: Es un método que devuelve una lista de cadenas de texto con los valores de las variables que constituyen un contraejemplo o un modelo del conjunto de premisas de entrada.
• Contains: Con esta función se comprueba si en una subrama existe la fórmula que se le pasa como parámetro, se puede usar para comprobar si una determinada regla se puede aplicar sobre la subrama, o bien para comprobar si la subrama está cerrada o se cerrará, pasándole la formula negada como parámetro.
• PerformStep: Se trata del método de más alto nivel, que se llama para que el Tableaux ejecute el siguiente paso. Devolverá true si se ha podido ejecutar un paso más, o false en caso contrario.
• WhatIf: Con este método comprobamos lo que pasaría en el Tableaux al aplicar una cierta regla en la rama actual. Devuelve un miembro de la enumeración StepResult, que puede valer NotAllowed, para indicar que no es posible realizar la operación, BranchClosed, para indicar que la rama se cerrará o None, para indicar que no sucederá nada relevante.

Los métodos CalcRect y Draw se utilizan simplemente para dibujar el esquema del Tableaux calculado.

La clase que administra el Tableaux es TableauxCalculator, a través del método Calculate.

Para terminar, te puedo recomendar el libro Lógica matemática para informáticos, en el que me he basado para implementar este desarrollo y en el que encontrarás muchos más temas relacionados con la lógica matemática y un buen número de ejemplos y ejercicios resueltos.